GraphMDN: Leveraging graph structure and deep learning to solve inverse problems

The recent introduction of Graph Neural Networks (GNNs) and their growing popularity in the past few years has enabled the application of deep learning algorithms to non-Euclidean, graph-structured data. GNNs have achieved state-of-the-art results across an impressive array of graph-based machine learning problems. Nevertheless, despite their rapid pace of development, much of the work on GNNs has focused on graph classification and embedding techniques, largely ignoring regression tasks over graph data. In this paper, we develop a Graph Mixture Density Network (GraphMDN), which combines graph neural networks with mixture density network (MDN) outputs. By combining these techniques, GraphMDNs have the advantage of naturally being able to incorporate graph structured information into a neural architecture, as well as the ability to model multi-modal regression targets. As such, GraphMDNs are designed to excel on regression tasks wherein the data are graph structured, and target statistics are better represented by mixtures of densities rather than singular values (so-called ``inverse problems"). To demonstrate this, we extend an existing GNN architecture known as Semantic GCN (SemGCN) to a GraphMDN structure, and show results from the Human3.6M pose estimation task. The extended model consistently outperforms both GCN and MDN architectures on their own, with a comparable number of parameters.

Autonomous Reinforcement of Behavioral Sequences in Neural Dynamics

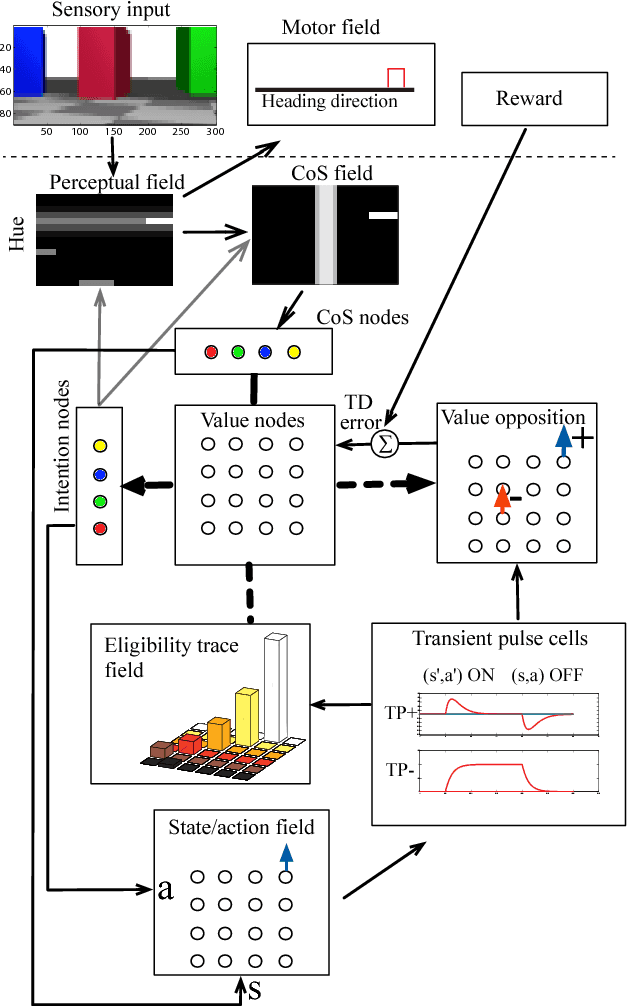
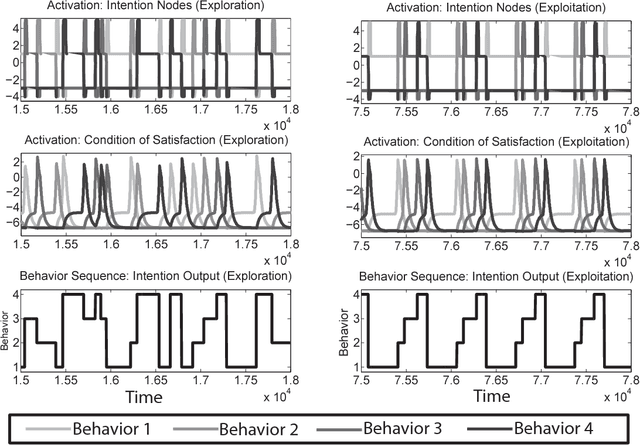
We introduce a dynamic neural algorithm called Dynamic Neural (DN) SARSA(\lambda) for learning a behavioral sequence from delayed reward. DN-SARSA(\lambda) combines Dynamic Field Theory models of behavioral sequence representation, classical reinforcement learning, and a computational neuroscience model of working memory, called Item and Order working memory, which serves as an eligibility trace. DN-SARSA(\lambda) is implemented on both a simulated and real robot that must learn a specific rewarding sequence of elementary behaviors from exploration. Results show DN-SARSA(\lambda) performs on the level of the discrete SARSA(\lambda), validating the feasibility of general reinforcement learning without compromising neural dynamics.