Application of Structured State Space Models to High energy physics with locality-sensitive hashing

Modern high-energy physics (HEP) experiments are increasingly challenged by the vast size and complexity of their datasets, particularly regarding large-scale point cloud processing and long sequences. In this study, to address these challenges, we explore the application of structured state space models (SSMs), proposing one of the first trials to integrate local-sensitive hashing into either a hybrid or pure Mamba Model. Our results demonstrate that pure SSMs could serve as powerful backbones for HEP problems involving tasks for long sequence data with local inductive bias. By integrating locality-sensitive hashing into Mamba blocks, we achieve significant improvements over traditional backbones in key HEP tasks, surpassing them in inference speed and physics metrics while reducing computational overhead. In key tests, our approach demonstrated promising results, presenting a viable alternative to traditional transformer backbones by significantly reducing FLOPS while maintaining robust performance.

BUFF: Boosted Decision Tree based Ultra-Fast Flow matching

Tabular data stands out as one of the most frequently encountered types in high energy physics. Unlike commonly homogeneous data such as pixelated images, simulating high-dimensional tabular data and accurately capturing their correlations are often quite challenging, even with the most advanced architectures. Based on the findings that tree-based models surpass the performance of deep learning models for tasks specific to tabular data, we adopt the very recent generative modeling class named conditional flow matching and employ different techniques to integrate the usage of Gradient Boosted Trees. The performances are evaluated for various tasks on different analysis level with several public datasets. We demonstrate the training and inference time of most high-level simulation tasks can achieve speedup by orders of magnitude. The application can be extended to low-level feature simulation and conditioned generations with competitive performance.

Particle Transformer for Jet Tagging

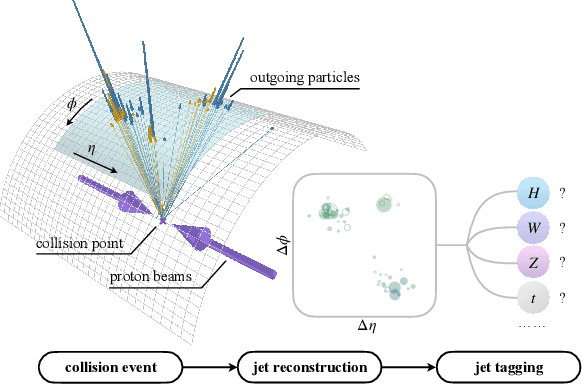
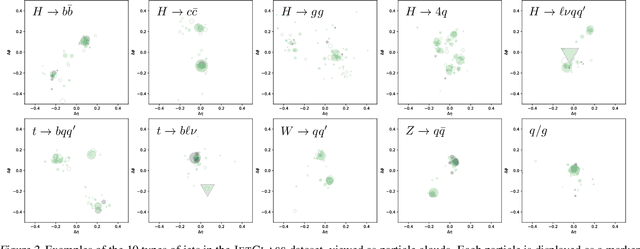
Jet tagging is a critical yet challenging classification task in particle physics. While deep learning has transformed jet tagging and significantly improved performance, the lack of a large-scale public dataset impedes further enhancement. In this work, we present JetClass, a new comprehensive dataset for jet tagging. The JetClass dataset consists of 100 M jets, about two orders of magnitude larger than existing public datasets. A total of 10 types of jets are simulated, including several types unexplored for tagging so far. Based on the large dataset, we propose a new Transformer-based architecture for jet tagging, called Particle Transformer (ParT). By incorporating pairwise particle interactions in the attention mechanism, ParT achieves higher tagging performance than a plain Transformer and surpasses the previous state-of-the-art, ParticleNet, by a large margin. The pre-trained ParT models, once fine-tuned, also substantially enhance the performance on two widely adopted jet tagging benchmarks.

Schrödinger PCA: You Only Need Variances for Eigenmodes

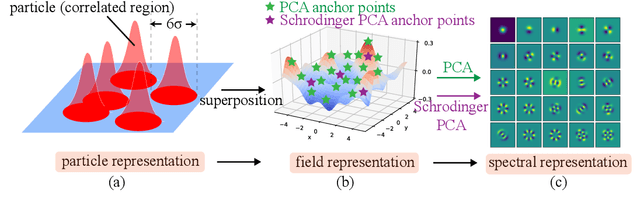
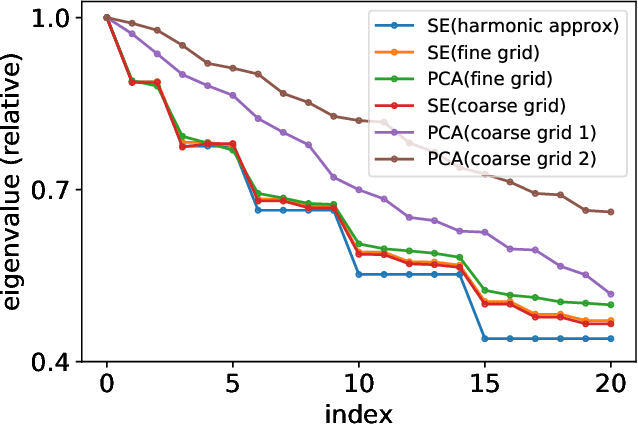
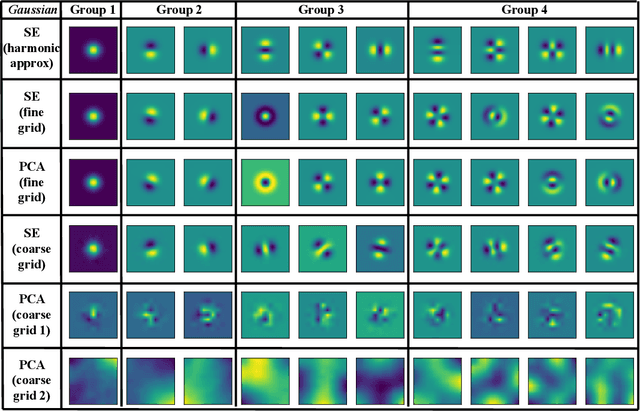
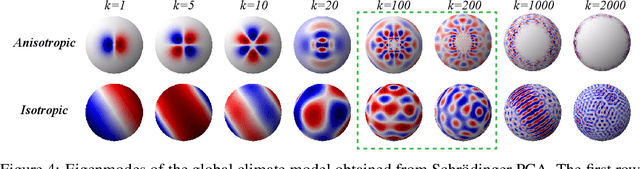
Principal component analysis (PCA) has achieved great success in unsupervised learning by identifying covariance correlations among features. If the data collection fails to capture the covariance information, PCA will not be able to discover meaningful modes. In particular, PCA will fail the spatial Gaussian Process (GP) model in the undersampling regime, i.e. the averaged distance of neighboring anchor points (spatial features) is greater than the correlation length of GP. Counterintuitively, by drawing the connection between PCA and Schr\"odinger equation, we can not only attack the undersampling challenge but also compute in an efficient and decoupled way with the proposed algorithm called Schr\"odinger PCA. Our algorithm only requires variances of features and estimated correlation length as input, constructs the corresponding Schr\"odinger equation, and solves it to obtain the energy eigenstates, which coincide with principal components. We will also establish the connection of our algorithm to the model reduction techniques in the partial differential equation (PDE) community, where the steady-state Schr\"odinger operator is identified as a second-order approximation to the covariance function. Numerical experiments are implemented to testify the validity and efficiency of the proposed algorithm, showing its potential for unsupervised learning tasks on general graphs and manifolds.