On the Quantification of Image Reconstruction Uncertainty without Training Data

Computational imaging plays a pivotal role in determining hidden information from sparse measurements. A robust inverse solver is crucial to fully characterize the uncertainty induced by these measurements, as it allows for the estimation of the complete posterior of unrecoverable targets. This, in turn, facilitates a probabilistic interpretation of observational data for decision-making. In this study, we propose a deep variational framework that leverages a deep generative model to learn an approximate posterior distribution to effectively quantify image reconstruction uncertainty without the need for training data. We parameterize the target posterior using a flow-based model and minimize their Kullback-Leibler (KL) divergence to achieve accurate uncertainty estimation. To bolster stability, we introduce a robust flow-based model with bi-directional regularization and enhance expressivity through gradient boosting. Additionally, we incorporate a space-filling design to achieve substantial variance reduction on both latent prior space and target posterior space. We validate our method on several benchmark tasks and two real-world applications, namely fastMRI and black hole image reconstruction. Our results indicate that our method provides reliable and high-quality image reconstruction with robust uncertainty estimation.

Accelerating Inverse Learning via Intelligent Localization with Exploratory Sampling

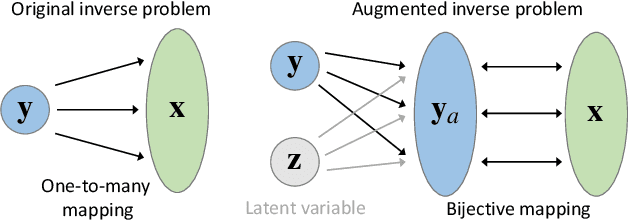
In the scope of "AI for Science", solving inverse problems is a longstanding challenge in materials and drug discovery, where the goal is to determine the hidden structures given a set of desirable properties. Deep generative models are recently proposed to solve inverse problems, but these currently use expensive forward operators and struggle in precisely localizing the exact solutions and fully exploring the parameter spaces without missing solutions. In this work, we propose a novel approach (called iPage) to accelerate the inverse learning process by leveraging probabilistic inference from deep invertible models and deterministic optimization via fast gradient descent. Given a target property, the learned invertible model provides a posterior over the parameter space; we identify these posterior samples as an intelligent prior initialization which enables us to narrow down the search space. We then perform gradient descent to calibrate the inverse solutions within a local region. Meanwhile, a space-filling sampling is imposed on the latent space to better explore and capture all possible solutions. We evaluate our approach on three benchmark tasks and two created datasets with real-world applications from quantum chemistry and additive manufacturing, and find our method achieves superior performance compared to several state-of-the-art baseline methods. The iPage code is available at https://github.com/jxzhangjhu/MatDesINNe.

Atomic structure generation from reconstructing structural fingerprints

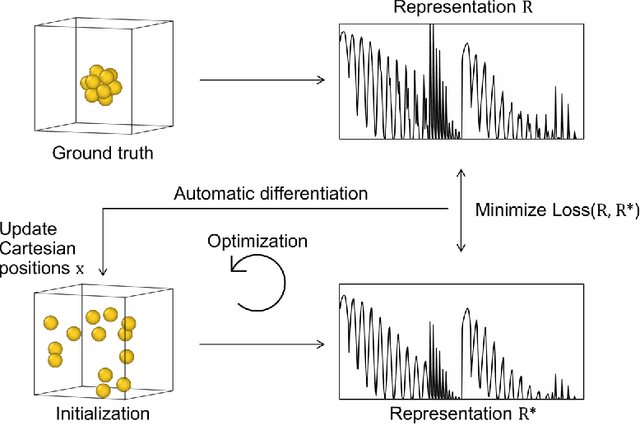
Data-driven machine learning methods have the potential to dramatically accelerate the rate of materials design over conventional human-guided approaches. These methods would help identify or, in the case of generative models, even create novel crystal structures of materials with a set of specified functional properties to then be synthesized or isolated in the laboratory. For crystal structure generation, a key bottleneck lies in developing suitable atomic structure fingerprints or representations for the machine learning model, analogous to the graph-based or SMILES representations used in molecular generation. However, finding data-efficient representations that are invariant to translations, rotations, and permutations, while remaining invertible to the Cartesian atomic coordinates remains an ongoing challenge. Here, we propose an alternative approach to this problem by taking existing non-invertible representations with the desired invariances and developing an algorithm to reconstruct the atomic coordinates through gradient-based optimization using automatic differentiation. This can then be coupled to a generative machine learning model which generates new materials within the representation space, rather than in the data-inefficient Cartesian space. In this work, we implement this end-to-end structure generation approach using atom-centered symmetry functions as the representation and conditional variational autoencoders as the generative model. We are able to successfully generate novel and valid atomic structures of sub-nanometer Pt nanoparticles as a proof of concept. Furthermore, this method can be readily extended to any suitable structural representation, thereby providing a powerful, generalizable framework towards structure-based generation.

A Hybrid Gradient Method to Designing Bayesian Experiments for Implicit Models

Bayesian experimental design (BED) aims at designing an experiment to maximize the information gathering from the collected data. The optimal design is usually achieved by maximizing the mutual information (MI) between the data and the model parameters. When the analytical expression of the MI is unavailable, e.g., having implicit models with intractable data distributions, a neural network-based lower bound of the MI was recently proposed and a gradient ascent method was used to maximize the lower bound. However, the approach in Kleinegesse et al., 2020 requires a pathwise sampling path to compute the gradient of the MI lower bound with respect to the design variables, and such a pathwise sampling path is usually inaccessible for implicit models. In this work, we propose a hybrid gradient approach that leverages recent advances in variational MI estimator and evolution strategies (ES) combined with black-box stochastic gradient ascent (SGA) to maximize the MI lower bound. This allows the design process to be achieved through a unified scalable procedure for implicit models without sampling path gradients. Several experiments demonstrate that our approach significantly improves the scalability of BED for implicit models in high-dimensional design space.

A Scalable Gradient-Free Method for Bayesian Experimental Design with Implicit Models

Bayesian experimental design (BED) is to answer the question that how to choose designs that maximize the information gathering. For implicit models, where the likelihood is intractable but sampling is possible, conventional BED methods have difficulties in efficiently estimating the posterior distribution and maximizing the mutual information (MI) between data and parameters. Recent work proposed the use of gradient ascent to maximize a lower bound on MI to deal with these issues. However, the approach requires a sampling path to compute the pathwise gradient of the MI lower bound with respect to the design variables, and such a pathwise gradient is usually inaccessible for implicit models. In this paper, we propose a novel approach that leverages recent advances in stochastic approximate gradient ascent incorporated with a smoothed variational MI estimator for efficient and robust BED. Without the necessity of pathwise gradients, our approach allows the design process to be achieved through a unified procedure with an approximate gradient for implicit models. Several experiments show that our approach outperforms baseline methods, and significantly improves the scalability of BED in high-dimensional problems.

Scalable Deep-Learning-Accelerated Topology Optimization for Additively Manufactured Materials

Topology optimization (TO) is a popular and powerful computational approach for designing novel structures, materials, and devices. Two computational challenges have limited the applicability of TO to a variety of industrial applications. First, a TO problem often involves a large number of design variables to guarantee sufficient expressive power. Second, many TO problems require a large number of expensive physical model simulations, and those simulations cannot be parallelized. To address these issues, we propose a general scalable deep-learning (DL) based TO framework, referred to as SDL-TO, which utilizes parallel schemes in high performance computing (HPC) to accelerate the TO process for designing additively manufactured (AM) materials. Unlike the existing studies of DL for TO, our framework accelerates TO by learning the iterative history data and simultaneously training on the mapping between the given design and its gradient. The surrogate gradient is learned by utilizing parallel computing on multiple CPUs incorporated with a distributed DL training on multiple GPUs. The learned TO gradient enables a fast online update scheme instead of an expensive update based on the physical simulator or solver. Using a local sampling strategy, we achieve to reduce the intrinsic high dimensionality of the design space and improve the training accuracy and the scalability of the SDL-TO framework. The method is demonstrated by benchmark examples and AM materials design for heat conduction. The proposed SDL-TO framework shows competitive performance compared to the baseline methods but significantly reduces the computational cost by a speed up of around 8.6x over the standard TO implementation.

Robust data-driven approach for predicting the configurational energy of high entropy alloys

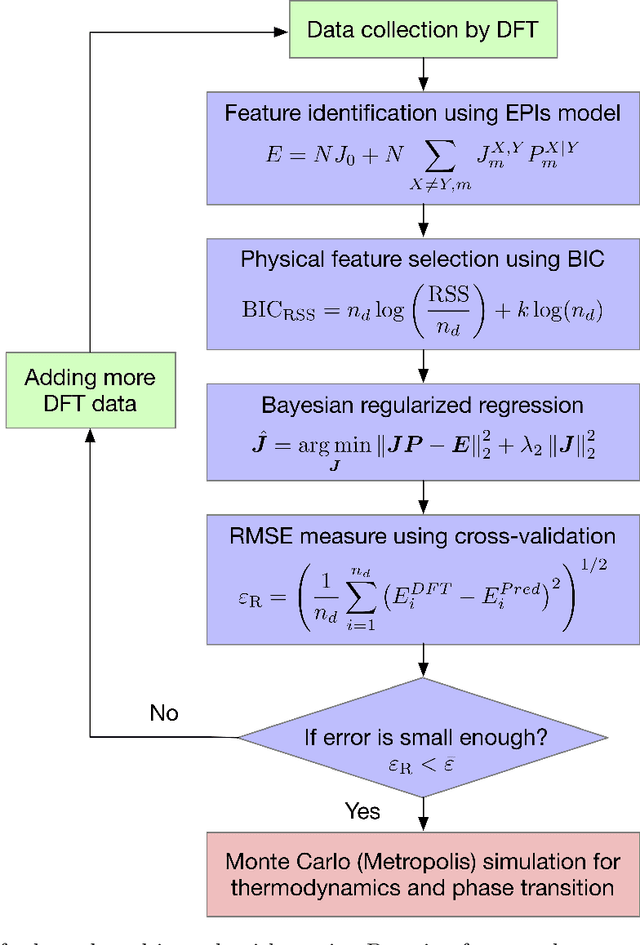
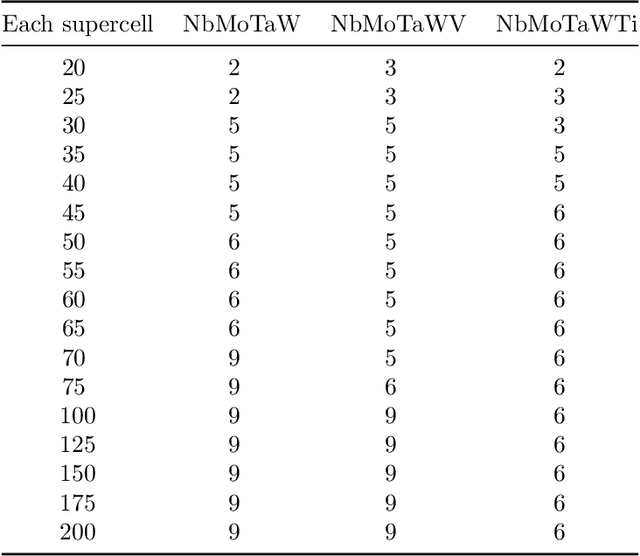
High entropy alloys (HEAs) have been increasingly attractive as promising next-generation materials due to their various excellent properties. It's necessary to essentially characterize the degree of chemical ordering and identify order-disorder transitions through efficient simulation and modeling of thermodynamics. In this study, a robust data-driven framework based on Bayesian approaches is proposed and demonstrated on the accurate and efficient prediction of configurational energy of high entropy alloys. The proposed effective pair interaction (EPI) model with ensemble sampling is used to map the configuration and its corresponding energy. Given limited data calculated by first-principles calculations, Bayesian regularized regression not only offers an accurate and stable prediction but also effectively quantifies the uncertainties associated with EPI parameters. Compared with the arbitrary determination of model complexity, we further conduct a physical feature selection to identify the truncation of coordination shells in EPI model using Bayesian information criterion. The results achieve efficient and robust performance in predicting the configurational energy, particularly given small data. The developed methodology is applied to study a series of refractory HEAs, i.e. NbMoTaW, NbMoTaWV and NbMoTaWTi where it is demonstrated how dataset size affects the confidence we can place in statistical estimates of configurational energy when data are sparse.