On Neural Estimators for Conditional Mutual Information Using Nearest Neighbors Sampling

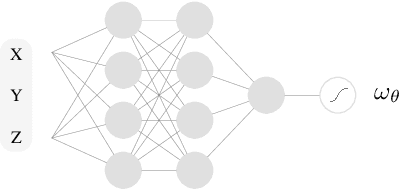
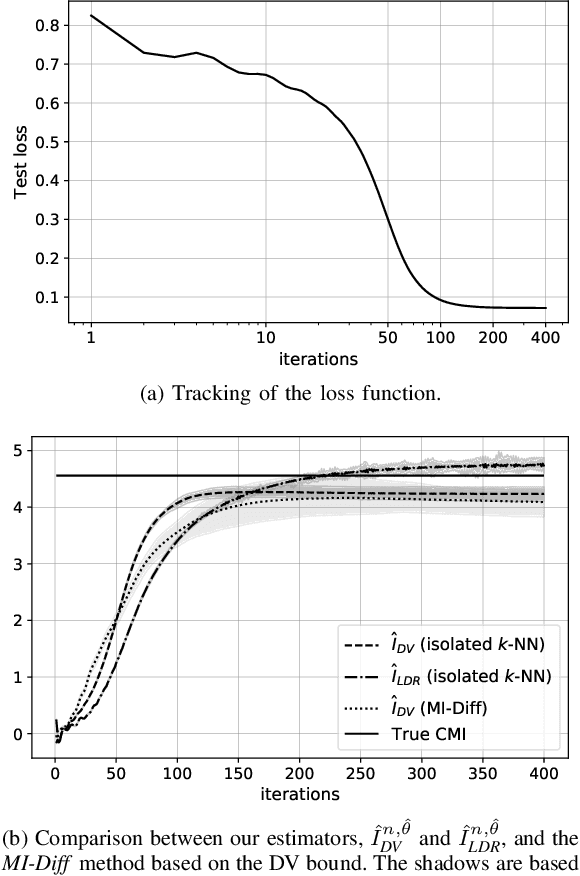
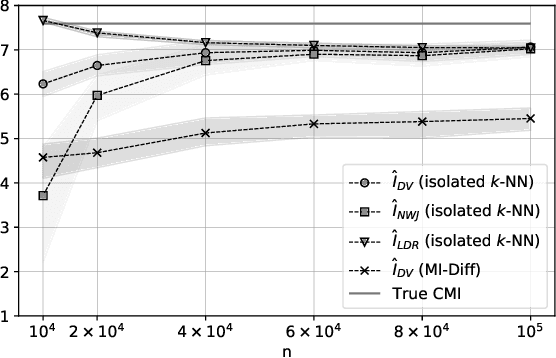
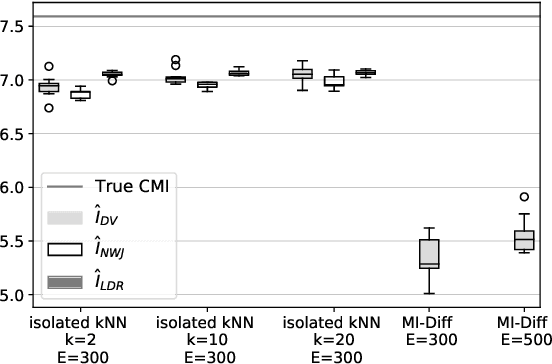
The estimation of mutual information (MI) or conditional mutual information (CMI) from a set of samples is a long-standing problem. A recent line of work in this area has leveraged the approximation power of artificial neural networks and has shown improvements over conventional methods. One important challenge in this new approach is the need to obtain, given the original dataset, a different set where the samples are distributed according to a specific product density function. This is particularly challenging when estimating CMI. In this paper, we introduce a new technique, based on k nearest neighbors (k-NN), to perform the resampling and derive high-confidence concentration bounds for the sample average. Then the technique is employed to train a neural network classifier and the CMI is estimated accordingly. We propose three estimators using this technique and prove their consistency, make a comparison between them and similar approaches in the literature, and experimentally show improvements in estimating the CMI in terms of accuracy and variance of the estimators.

Conditional Mutual Information Neural Estimator

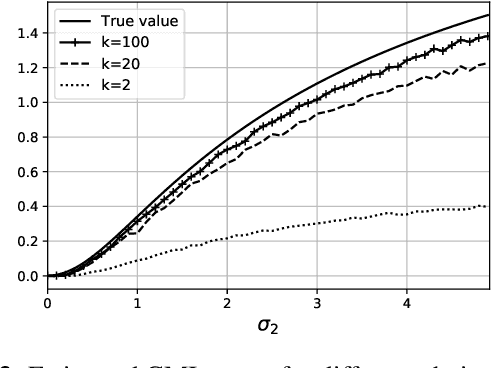
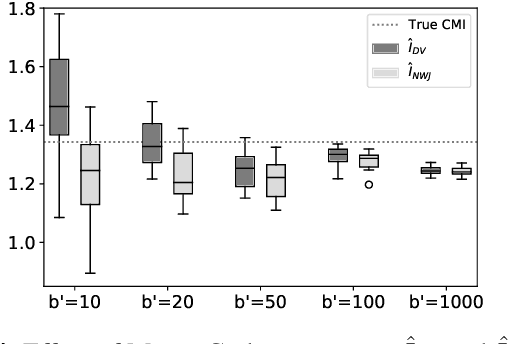
Several recent works in communication systems have proposed to leverage the power of neural networks in the design of encoders and decoders. In this approach, these blocks can be tailored to maximize the transmission rate based on aggregated samples from the channel. Motivated by the fact that, in many communication schemes, the achievable transmission rate is determined by a conditional mutual information, this paper focuses on neural-based estimators for this information-theoretic quantity. Our results are based on variational bounds for the KL-divergence and, in contrast to some previous works, we provide a mathematically rigorous lower bound. However, additional challenges with respect to the unconditional mutual information emerge due to the presence of a conditional density function; this is also addressed here.