Conditional Mutual Information Neural Estimator
Paper and Code
Nov 06, 2019

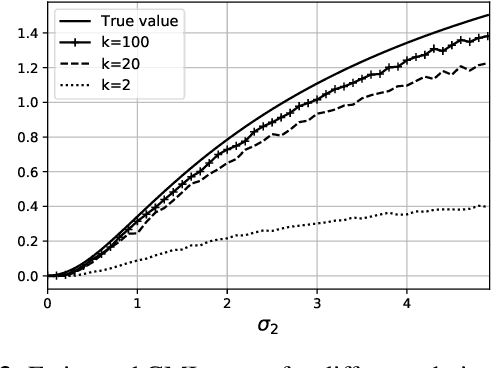
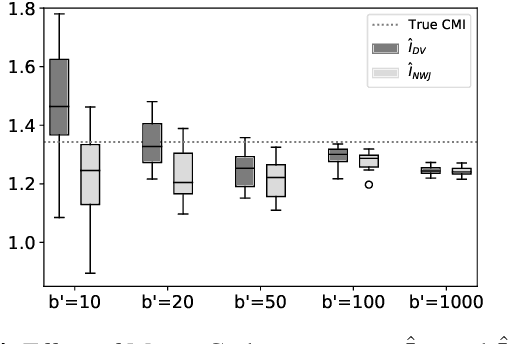
Several recent works in communication systems have proposed to leverage the power of neural networks in the design of encoders and decoders. In this approach, these blocks can be tailored to maximize the transmission rate based on aggregated samples from the channel. Motivated by the fact that, in many communication schemes, the achievable transmission rate is determined by a conditional mutual information, this paper focuses on neural-based estimators for this information-theoretic quantity. Our results are based on variational bounds for the KL-divergence and, in contrast to some previous works, we provide a mathematically rigorous lower bound. However, additional challenges with respect to the unconditional mutual information emerge due to the presence of a conditional density function; this is also addressed here.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge