Scalable Nonparametric Sampling from Multimodal Posteriors with the Posterior Bootstrap

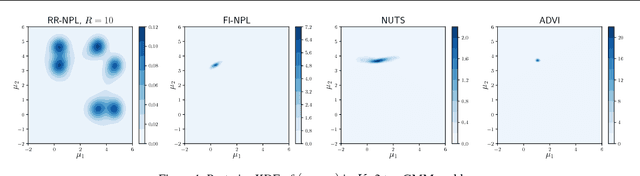
Increasingly complex datasets pose a number of challenges for Bayesian inference. Conventional posterior sampling based on Markov chain Monte Carlo can be too computationally intensive, is serial in nature and mixes poorly between posterior modes. Further, all models are misspecified, which brings into question the validity of the conventional Bayesian update. We present a scalable Bayesian nonparametric learning routine that enables posterior sampling through the optimization of suitably randomized objective functions. A Dirichlet process prior on the unknown data distribution accounts for model misspecification, and admits an embarrassingly parallel posterior bootstrap algorithm that generates independent and exact samples from the nonparametric posterior distribution. Our method is particularly adept at sampling from multimodal posterior distributions via a random restart mechanism. We demonstrate our method on Gaussian mixture model and sparse logistic regression examples.

General Bayesian Updating and the Loss-Likelihood Bootstrap

In this paper we revisit the weighted likelihood bootstrap, a method that generates samples from an approximate Bayesian posterior of a parametric model. We show that the same method can be derived, without approximation, under a Bayesian nonparametric model with the parameter of interest defined as minimising an expected negative log-likelihood under an unknown sampling distribution. This interpretation enables us to extend the weighted likelihood bootstrap to posterior sampling for parameters minimizing an expected loss. We call this method the loss-likelihood bootstrap. We make a connection between this and general Bayesian updating, which is a way of updating prior belief distributions without needing to construct a global probability model, yet requires the calibration of two forms of loss function. The loss-likelihood bootstrap is used to calibrate the general Bayesian posterior by matching asymptotic Fisher information. We demonstrate the methodology on a number of examples.