Measurement-based Admission Control in Sliced Networks: A Best Arm Identification Approach

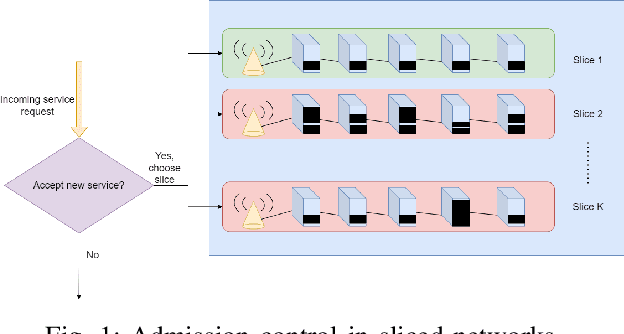
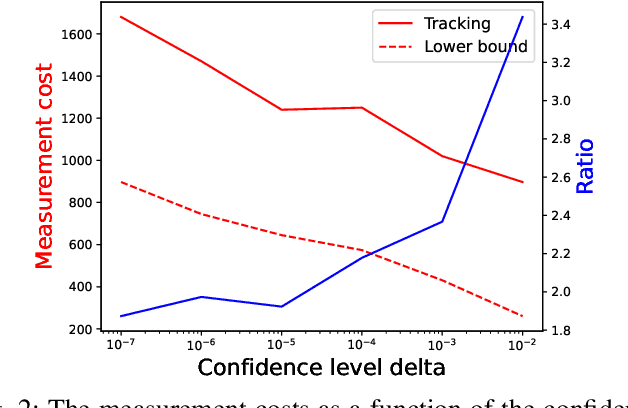
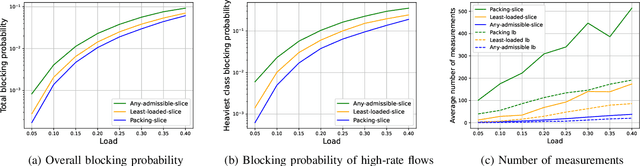
In sliced networks, the shared tenancy of slices requires adaptive admission control of data flows, based on measurements of network resources. In this paper, we investigate the design of measurement-based admission control schemes, deciding whether a new data flow can be admitted and in this case, on which slice. The objective is to devise a joint measurement and decision strategy that returns a correct decision (e.g., the least loaded slice) with a certain level of confidence while minimizing the measurement cost (the number of measurements made before committing to the decision). We study the design of such strategies for several natural admission criteria specifying what a correct decision is. For each of these criteria, using tools from best arm identification in bandits, we first derive an explicit information-theoretical lower bound on the cost of any algorithm returning the correct decision with fixed confidence. We then devise a joint measurement and decision strategy achieving this theoretical limit. We compare empirically the measurement costs of these strategies, and compare them both to the lower bounds as well as a naive measurement scheme. We find that our algorithm significantly outperforms the naive scheme (by a factor $2-8$).

Predictive Bandits

We introduce and study a new class of stochastic bandit problems, referred to as predictive bandits. In each round, the decision maker first decides whether to gather information about the rewards of particular arms (so that their rewards in this round can be predicted). These measurements are costly, and may be corrupted by noise. The decision maker then selects an arm to be actually played in the round. Predictive bandits find applications in many areas; e.g. they can be applied to channel selection problems in radio communication systems. In this paper, we provide the first theoretical results about predictive bandits, and focus on scenarios where the decision maker is allowed to measure at most one arm per round. We derive asymptotic instance-specific regret lower bounds for these problems, and develop algorithms whose regret match these fundamental limits. We illustrate the performance of our algorithms through numerical experiments. In particular, we highlight the gains that can be achieved by using reward predictions, and investigate the impact of the noise in the corresponding measurements.