Measurement-based Admission Control in Sliced Networks: A Best Arm Identification Approach
Paper and Code
Apr 14, 2022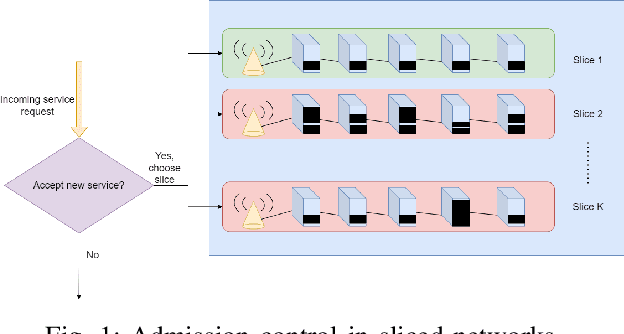
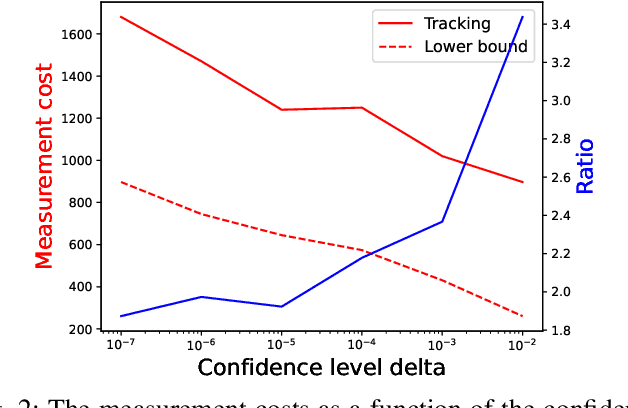
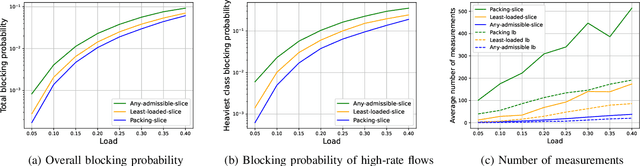

In sliced networks, the shared tenancy of slices requires adaptive admission control of data flows, based on measurements of network resources. In this paper, we investigate the design of measurement-based admission control schemes, deciding whether a new data flow can be admitted and in this case, on which slice. The objective is to devise a joint measurement and decision strategy that returns a correct decision (e.g., the least loaded slice) with a certain level of confidence while minimizing the measurement cost (the number of measurements made before committing to the decision). We study the design of such strategies for several natural admission criteria specifying what a correct decision is. For each of these criteria, using tools from best arm identification in bandits, we first derive an explicit information-theoretical lower bound on the cost of any algorithm returning the correct decision with fixed confidence. We then devise a joint measurement and decision strategy achieving this theoretical limit. We compare empirically the measurement costs of these strategies, and compare them both to the lower bounds as well as a naive measurement scheme. We find that our algorithm significantly outperforms the naive scheme (by a factor $2-8$).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge