One-step Bipartite Graph Cut: A Normalized Formulation and Its Application to Scalable Subspace Clustering

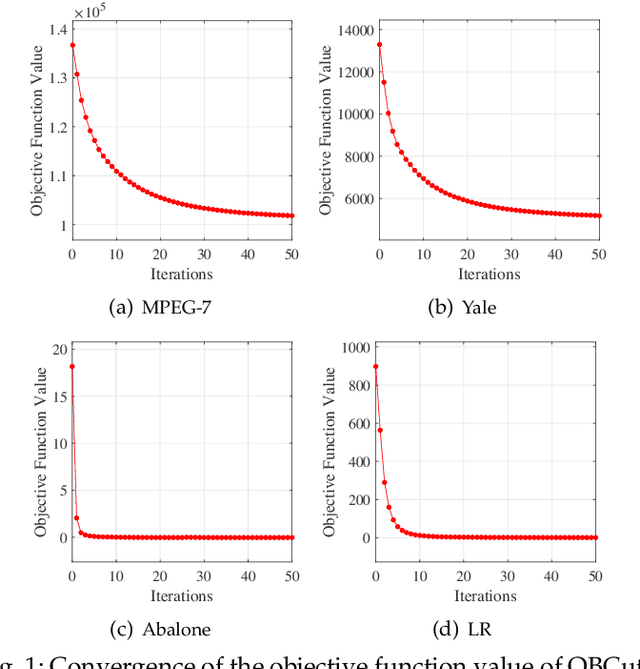
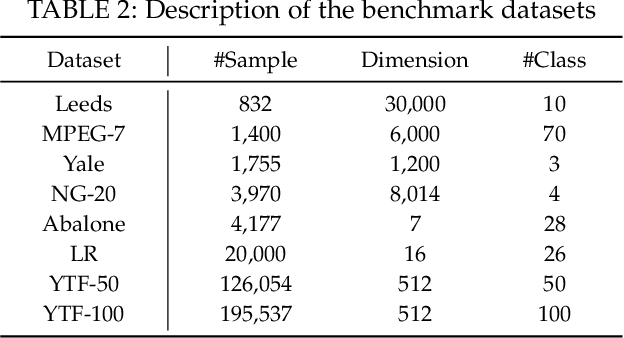
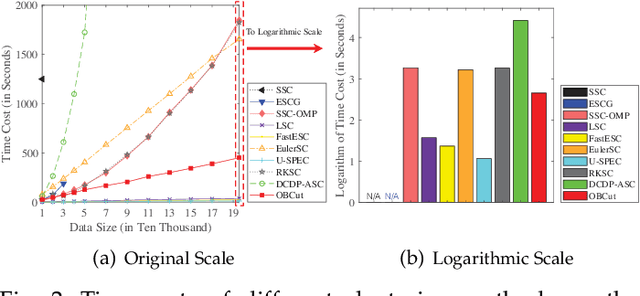
The bipartite graph structure has shown its promising ability in facilitating the subspace clustering and spectral clustering algorithms for large-scale datasets. To avoid the post-processing via k-means during the bipartite graph partitioning, the constrained Laplacian rank (CLR) is often utilized for constraining the number of connected components (i.e., clusters) in the bipartite graph, which, however, neglects the distribution (or normalization) of these connected components and may lead to imbalanced or even ill clusters. Despite the significant success of normalized cut (Ncut) in general graphs, it remains surprisingly an open problem how to enforce a one-step normalized cut for bipartite graphs, especially with linear-time complexity. In this paper, we first characterize a novel one-step bipartite graph cut (OBCut) criterion with normalized constraints, and theoretically prove its equivalence to a trace maximization problem. Then we extend this cut criterion to a scalable subspace clustering approach, where adaptive anchor learning, bipartite graph learning, and one-step normalized bipartite graph partitioning are simultaneously modeled in a unified objective function, and an alternating optimization algorithm is further designed to solve it in linear time. Experiments on a variety of general and large-scale datasets demonstrate the effectiveness and scalability of our approach.

Efficient Multi-view Clustering via Unified and Discrete Bipartite Graph Learning

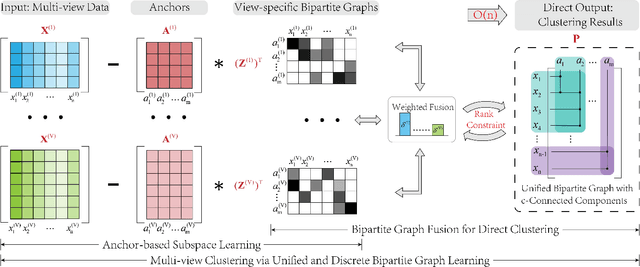
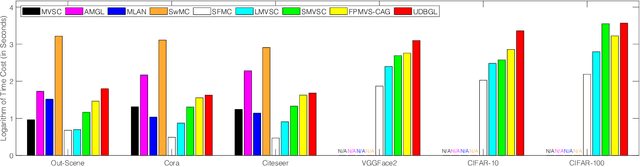
Although previous graph-based multi-view clustering algorithms have gained significant progress, most of them are still faced with three limitations. First, they often suffer from high computational complexity, which restricts their applications in large-scale scenarios. Second, they usually perform graph learning either at the single-view level or at the view-consensus level, but often neglect the possibility of the joint learning of single-view and consensus graphs. Third, many of them rely on the $k$-means for discretization of the spectral embeddings, which lack the ability to directly learn the graph with discrete cluster structure. In light of this, this paper presents an efficient multi-view clustering approach via unified and discrete bipartite graph learning (UDBGL). Specifically, the anchor-based subspace learning is incorporated to learn the view-specific bipartite graphs from multiple views, upon which the bipartite graph fusion is leveraged to learn a view-consensus bipartite graph with adaptive weight learning. Further, the Laplacian rank constraint is imposed to ensure that the fused bipartite graph has discrete cluster structures (with a specific number of connected components). By simultaneously formulating the view-specific bipartite graph learning, the view-consensus bipartite graph learning, and the discrete cluster structure learning into a unified objective function, an efficient minimization algorithm is then designed to tackle this optimization problem and directly achieve a discrete clustering solution without requiring additional partitioning, which notably has linear time complexity in data size. Experiments on a variety of multi-view datasets demonstrate the robustness and efficiency of our UDBGL approach.

Joint Multi-view Unsupervised Feature Selection and Graph Learning

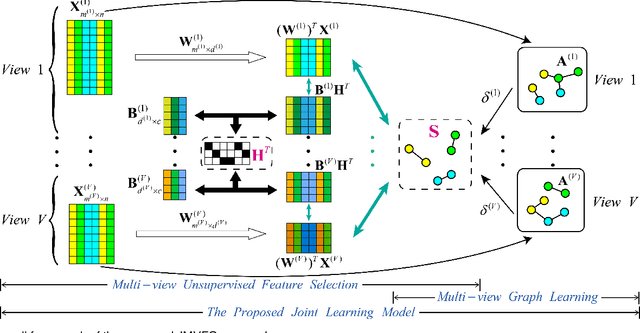
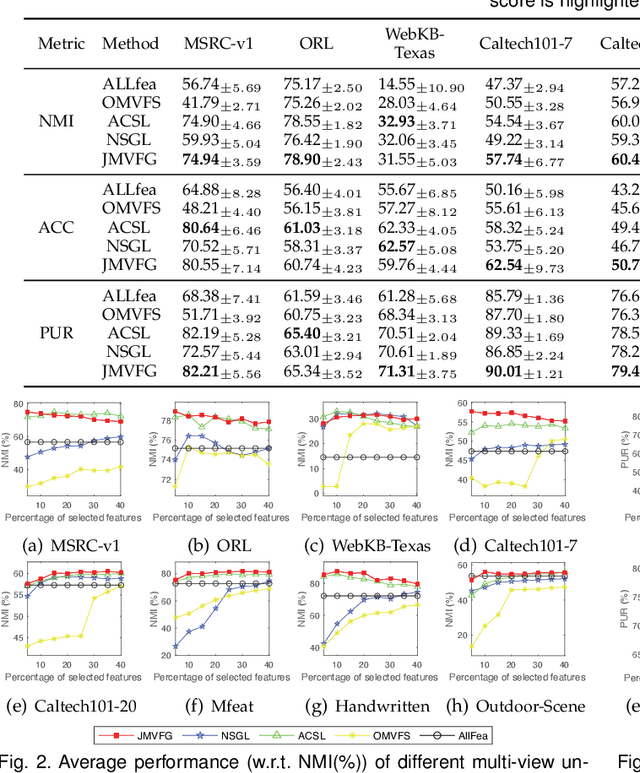
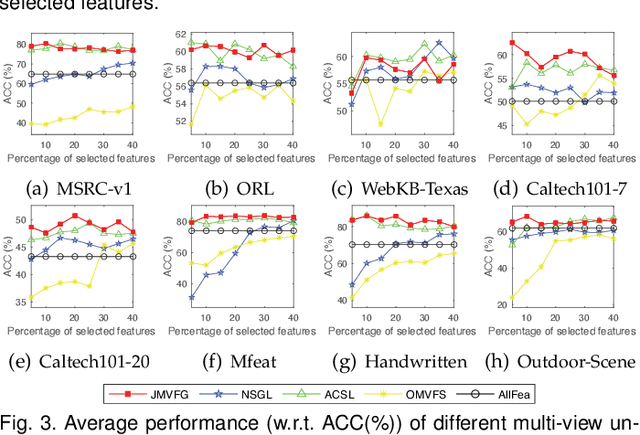
Despite the recent progress, the existing multi-view unsupervised feature selection methods mostly suffer from two limitations. First, they generally utilize either cluster structure or similarity structure to guide the feature selection, neglecting the possibility of a joint formulation with mutual benefits. Second, they often learn the similarity structure by either global structure learning or local structure learning, lacking the capability of graph learning with both global and local structural awareness. In light of this, this paper presents a joint multi-view unsupervised feature selection and graph learning (JMVFG) approach. Particularly, we formulate the multi-view feature selection with orthogonal decomposition, where each target matrix is decomposed into a view-specific basis matrix and a view-consistent cluster indicator. Cross-space locality preservation is incorporated to bridge the cluster structure learning in the projected space and the similarity learning (i.e., graph learning) in the original space. Further, a unified objective function is presented to enable the simultaneous learning of the cluster structure, the global and local similarity structures, and the multi-view consistency and inconsistency, upon which an alternating optimization algorithm is developed with theoretically proved convergence. Extensive experiments demonstrate the superiority of our approach for both multi-view feature selection and graph learning tasks.