One-step Bipartite Graph Cut: A Normalized Formulation and Its Application to Scalable Subspace Clustering
Paper and Code
May 12, 2023
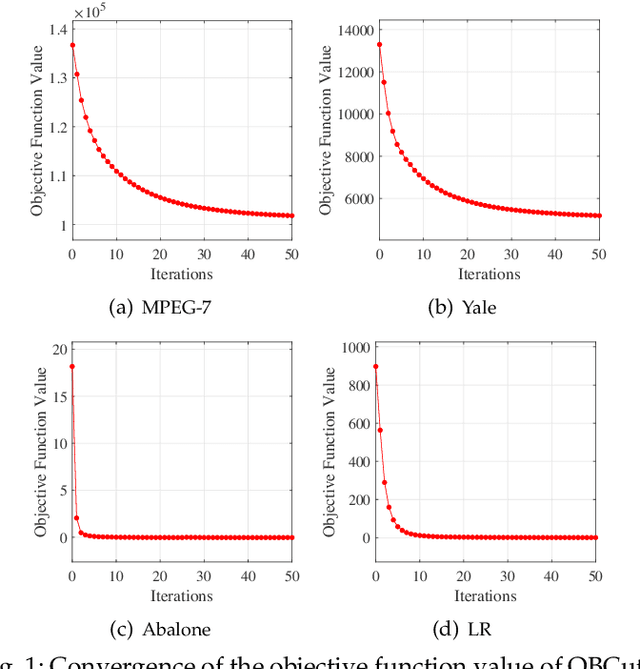
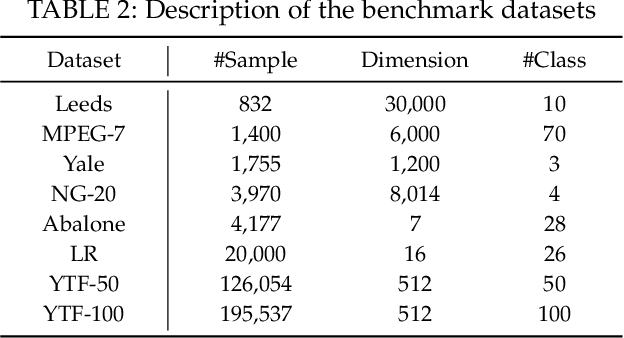
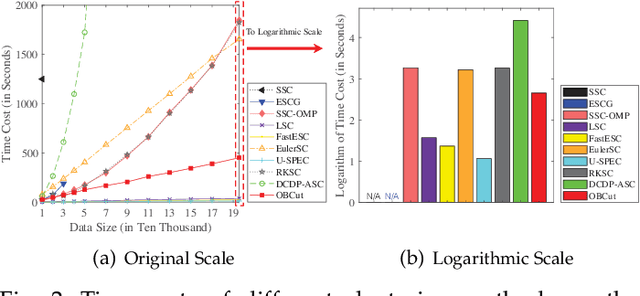
The bipartite graph structure has shown its promising ability in facilitating the subspace clustering and spectral clustering algorithms for large-scale datasets. To avoid the post-processing via k-means during the bipartite graph partitioning, the constrained Laplacian rank (CLR) is often utilized for constraining the number of connected components (i.e., clusters) in the bipartite graph, which, however, neglects the distribution (or normalization) of these connected components and may lead to imbalanced or even ill clusters. Despite the significant success of normalized cut (Ncut) in general graphs, it remains surprisingly an open problem how to enforce a one-step normalized cut for bipartite graphs, especially with linear-time complexity. In this paper, we first characterize a novel one-step bipartite graph cut (OBCut) criterion with normalized constraints, and theoretically prove its equivalence to a trace maximization problem. Then we extend this cut criterion to a scalable subspace clustering approach, where adaptive anchor learning, bipartite graph learning, and one-step normalized bipartite graph partitioning are simultaneously modeled in a unified objective function, and an alternating optimization algorithm is further designed to solve it in linear time. Experiments on a variety of general and large-scale datasets demonstrate the effectiveness and scalability of our approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge