GMC-PINNs: A new general Monte Carlo PINNs method for solving fractional partial differential equations on irregular domains

Physics-Informed Neural Networks (PINNs) have been widely used for solving partial differential equations (PDEs) of different types, including fractional PDEs (fPDES) [29]. Herein, we propose a new general (quasi) Monte Carlo PINN for solving fPDEs on irregular domains. Specifically, instead of approximating fractional derivatives by Monte Carlo approximations of integrals as was done previously in [31], we use a more general Monte Carlo approximation method to solve different fPDEs, which is valid for fractional differentiation under any definition. Moreover, based on the ensemble probability density function, the generated nodes are all located in denser regions near the target point where we perform the differentiation. This has an unexpected connection with known finite difference methods on non-equidistant or nested grids, and hence our method inherits their advantages. At the same time, the generated nodes exhibit a block-like dense distribution, leading to a good computational efficiency of this approach. We present the framework for using this algorithm and apply it to several examples. Our results demonstrate the effectiveness of GMC-PINNs in dealing with irregular domain problems and show a higher computational efficiency compared to the original fPINN method. We also include comparisons with the Monte Carlo fPINN [31]. Finally, we use examples to demonstrate the effectiveness of the method in dealing with fuzzy boundary location problems, and then use the method to solve the coupled 3D fractional Bloch-Torrey equation defined in the ventricular domain of the human brain, and compare the results with classical numerical methods.

Iterative Network Pruning with Uncertainty Regularization for Lifelong Sentiment Classification

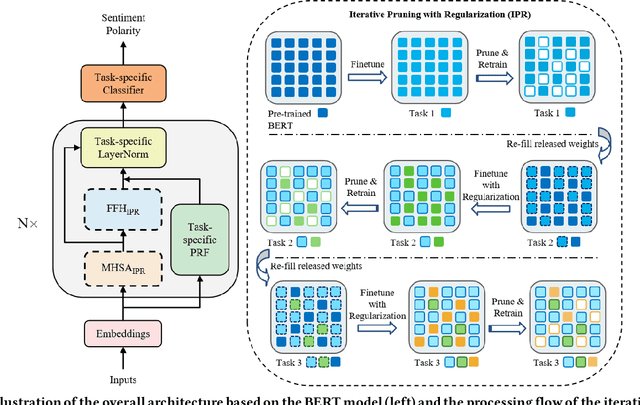
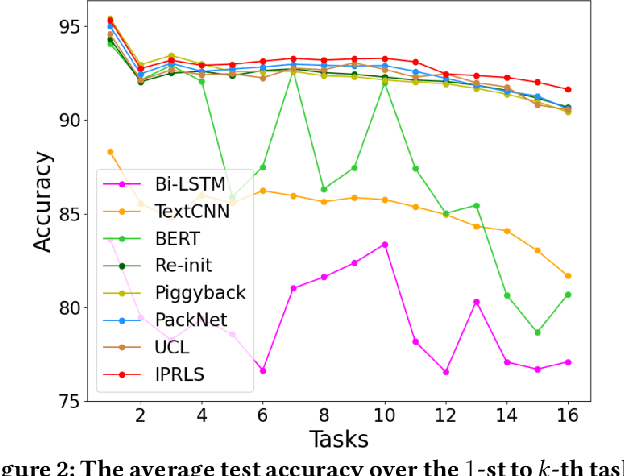
Lifelong learning capabilities are crucial for sentiment classifiers to process continuous streams of opinioned information on the Web. However, performing lifelong learning is non-trivial for deep neural networks as continually training of incrementally available information inevitably results in catastrophic forgetting or interference. In this paper, we propose a novel iterative network pruning with uncertainty regularization method for lifelong sentiment classification (IPRLS), which leverages the principles of network pruning and weight regularization. By performing network pruning with uncertainty regularization in an iterative manner, IPRLS can adapta single BERT model to work with continuously arriving data from multiple domains while avoiding catastrophic forgetting and interference. Specifically, we leverage an iterative pruning method to remove redundant parameters in large deep networks so that the freed-up space can then be employed to learn new tasks, tackling the catastrophic forgetting problem. Instead of keeping the old-tasks fixed when learning new tasks, we also use an uncertainty regularization based on the Bayesian online learning framework to constrain the update of old tasks weights in BERT, which enables positive backward transfer, i.e. learning new tasks improves performance on past tasks while protecting old knowledge from being lost. In addition, we propose a task-specific low-dimensional residual function in parallel to each layer of BERT, which makes IPRLS less prone to losing the knowledge saved in the base BERT network when learning a new task. Extensive experiments on 16 popular review corpora demonstrate that the proposed IPRLS method sig-nificantly outperforms the strong baselines for lifelong sentiment classification. For reproducibility, we submit the code and data at:https://github.com/siat-nlp/IPRLS.