Interpretable Price Bounds Estimation with Shape Constraints in Price Optimization

This paper addresses the interpretable estimation of price bounds within the context of price optimization. In recent years, price optimization methods have become indispensable for maximizing revenues and profits. However, effectively applying these methods to real-world pricing operations remains a significant challenge. It is crucial for operators, who are responsible for setting prices, to utilize reasonable price bounds that are not only interpretable but also acceptable. Despite this necessity, most studies assume that price bounds are given constant values, and few have explored the reasonable determination of these bounds. In response, we propose a comprehensive framework for determining price bounds, which includes both the estimation and adjustment of these bounds. Specifically, we first estimate the price bounds using three distinct approaches based on historical pricing data. We then adjust the estimated price bounds by solving an optimization problem that incorporates shape constraints. This method allows for the implementation of price optimization under practical and reasonable price bounds, suitable for real-world applications. We report the effectiveness of our proposed method through numerical experiments conducted with historical pricing data from actual services.

Coordinate descent heuristics for the irregular strip packing problem of rasterized shapes

We consider the irregular strip packing problem of rasterized shapes, where a given set of pieces of irregular shapes represented in pixels should be placed into a rectangular container without overlap. The rasterized shapes enable us to check overlap without any exceptional handling due to geometric issues, while they often require much memory and computational effort in high-resolution. We develop an efficient algorithm to check overlap using a pair of scanlines that reduces the complexity of rasterized shapes by merging consecutive pixels in each row and column into strips with unit width, respectively. Based on this, we develop coordinate descent heuristics that repeat a line search in the horizontal and vertical directions alternately. Computational results for test instances show that the proposed algorithm obtains sufficiently dense layouts of rasterized shapes in high-resolution within a reasonable computation time.

An efficient branch-and-cut algorithm for approximately submodular function maximization

When approaching to problems in computer science, we often encounter situations where a subset of a finite set maximizing some utility function needs to be selected. Some of such utility functions are known to be approximately submodular. For the problem of maximizing an approximately submodular function (ASFM problem), a greedy algorithm quickly finds good feasible solutions for many instances while guaranteeing ($1-e^{-\gamma}$)-approximation ratio for a given submodular ratio $\gamma$. However, we still encounter its applications that ask more accurate or exactly optimal solutions within a reasonable computation time. In this paper, we present an efficient branch-and-cut algorithm for the non-decreasing ASFM problem based on its binary integer programming (BIP) formulation with an exponential number of constraints. To this end, we first derive a BIP formulation of the ASFM problem and then, develop an improved constraint generation algorithm that starts from a reduced BIP problem with a small subset of constraints and repeats solving the reduced BIP problem while adding a promising set of constraints at each iteration. Moreover, we incorporate it into a branch-and-cut algorithm to attain good upper bounds while solving a smaller number of nodes of a search tree. The computational results for three types of well-known benchmark instances show that our algorithm performs better than the conventional exact algorithms.

An efficient branch-and-bound algorithm for submodular function maximization

The submodular function maximization is an attractive optimization model that appears in many real applications. Although a variety of greedy algorithms quickly find good feasible solutions for many instances while guaranteeing (1-1/e)-approximation ratio, we still encounter many real applications that ask optimal or better feasible solutions within reasonable computation time. In this paper, we present an efficient branch-and-bound algorithm for the non-decreasing submodular function maximization problem based on its binary integer programming (BIP) formulation with a huge number of constraints. Nemhauser and Wolsey developed an exact algorithm called the constraint generation algorithm that starts from a reduced BIP problem with a small subset of constraints taken from the constraints and repeats solving a reduced BIP problem while adding a new constraint at each iteration. However, their algorithm is still computationally expensive due to many reduced BIP problems to be solved. To overcome this, we propose an improved constraint generation algorithm to add a promising set of constraints at each iteration. We incorporate it into a branch-and-bound algorithm to attain good upper bounds while solving a smaller number of reduced BIP problems. According to computational results for well-known benchmark instances, our algorithm achieved better performance than the state-of-the-art exact algorithms.

Relaxation heuristics for the set multicover problem with generalized upper bound constraints

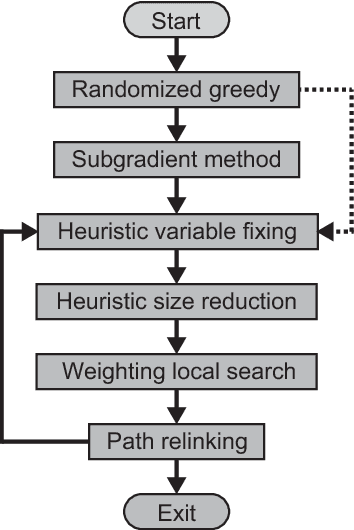
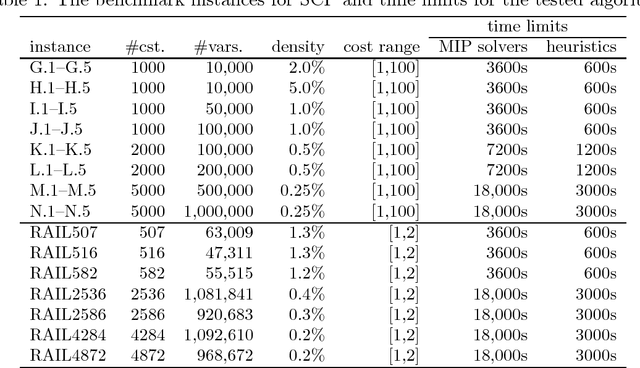
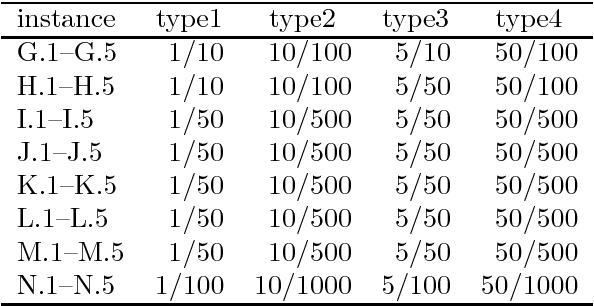
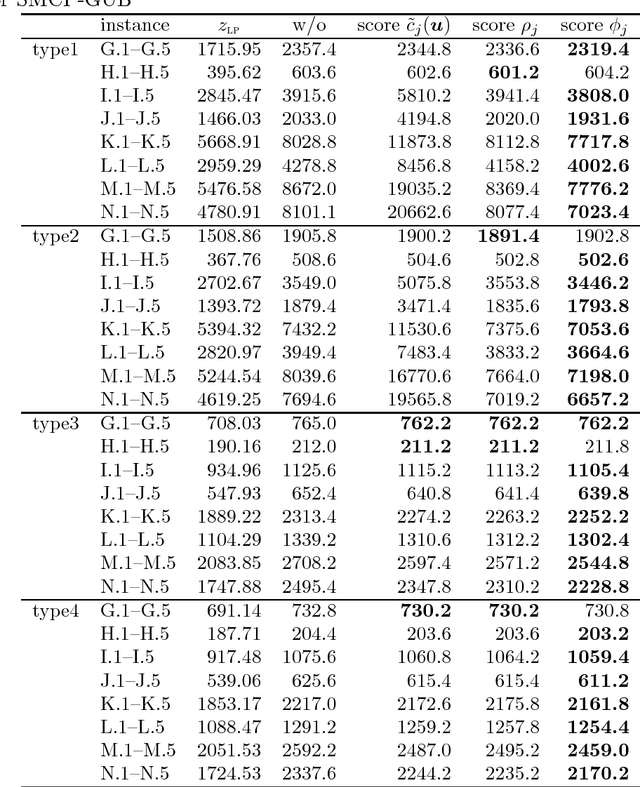
We consider an extension of the set covering problem (SCP) introducing (i)~multicover and (ii)~generalized upper bound (GUB)~constraints. For the conventional SCP, the pricing method has been introduced to reduce the size of instances, and several efficient heuristic algorithms based on such reduction techniques have been developed to solve large-scale instances. However, GUB constraints often make the pricing method less effective, because they often prevent solutions from containing highly evaluated variables together. To overcome this problem, we develop heuristic algorithms to reduce the size of instances, in which new evaluation schemes of variables are introduced taking account of GUB constraints. We also develop an efficient implementation of a 2-flip neighborhood local search algorithm that reduces the number of candidates in the neighborhood without sacrificing the solution quality. In order to guide the search to visit a wide variety of good solutions, we also introduce a path relinking method that generates new solutions by combining two or more solutions obtained so far. According to computational comparison on benchmark instances, the proposed method succeeds in selecting a small number of promising variables properly and performs quite effectively even for large-scale instances having hard GUB constraints.

Exploiting variable associations to configure efficient local search algorithms in large-scale binary integer programs

We present a data mining approach for reducing the search space of local search algorithms in a class of binary integer programs including the set covering and partitioning problems. The quality of locally optimal solutions typically improves if a larger neighborhood is used, while the computation time of searching the neighborhood increases exponentially. To overcome this, we extract variable associations from the instance to be solved in order to identify promising pairs of flipping variables in the neighborhood search. Based on this, we develop a 4-flip neighborhood local search algorithm that incorporates an efficient incremental evaluation of solutions and an adaptive control of penalty weights. Computational results show that the proposed method improves the performance of the local search algorithm for large-scale set covering and partitioning problems.