Relaxation heuristics for the set multicover problem with generalized upper bound constraints
Paper and Code
Jan 06, 2018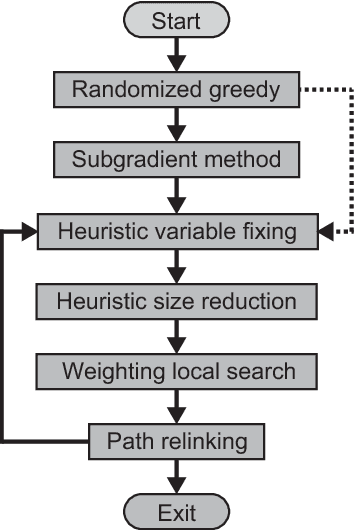
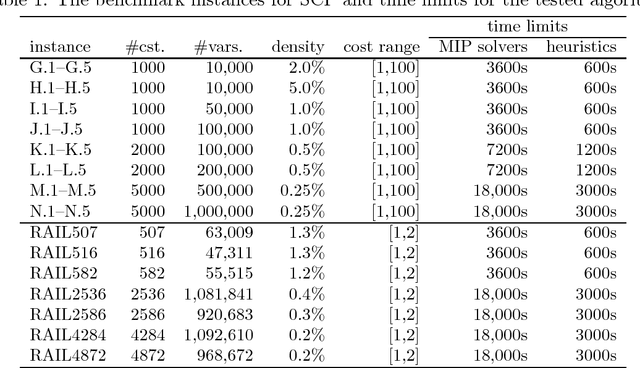
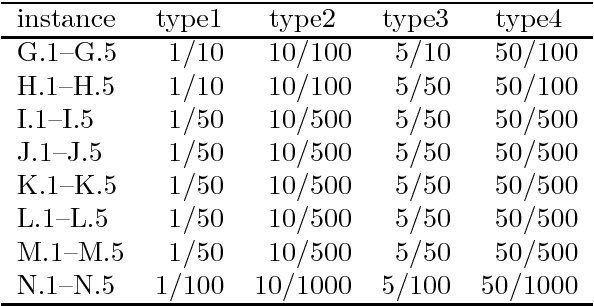
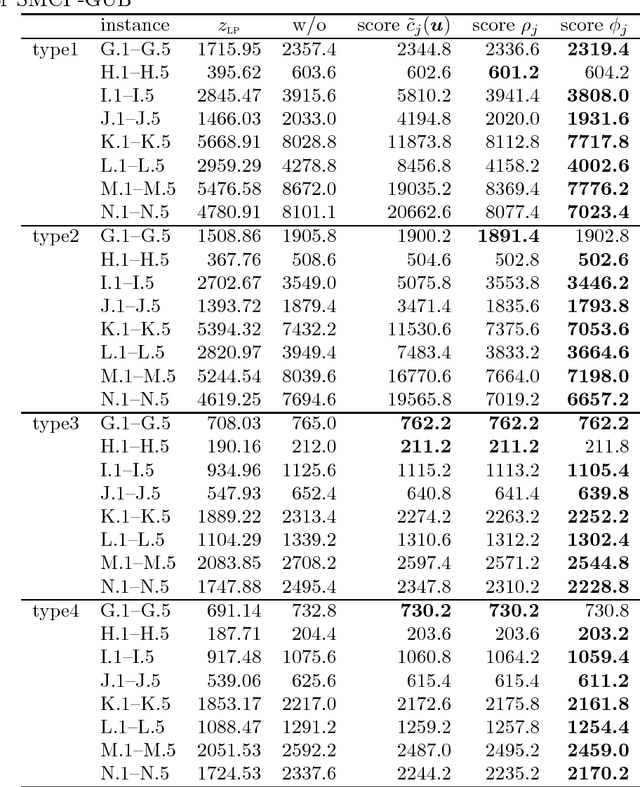
We consider an extension of the set covering problem (SCP) introducing (i)~multicover and (ii)~generalized upper bound (GUB)~constraints. For the conventional SCP, the pricing method has been introduced to reduce the size of instances, and several efficient heuristic algorithms based on such reduction techniques have been developed to solve large-scale instances. However, GUB constraints often make the pricing method less effective, because they often prevent solutions from containing highly evaluated variables together. To overcome this problem, we develop heuristic algorithms to reduce the size of instances, in which new evaluation schemes of variables are introduced taking account of GUB constraints. We also develop an efficient implementation of a 2-flip neighborhood local search algorithm that reduces the number of candidates in the neighborhood without sacrificing the solution quality. In order to guide the search to visit a wide variety of good solutions, we also introduce a path relinking method that generates new solutions by combining two or more solutions obtained so far. According to computational comparison on benchmark instances, the proposed method succeeds in selecting a small number of promising variables properly and performs quite effectively even for large-scale instances having hard GUB constraints.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge