Shruti Yadav Narayana
Hypervector Design for Efficient Hyperdimensional Computing on Edge Devices
Mar 08, 2021
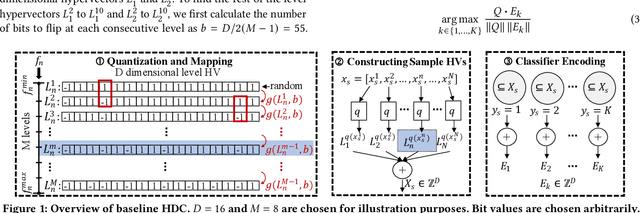
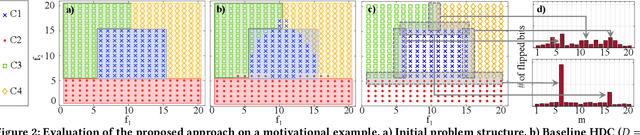
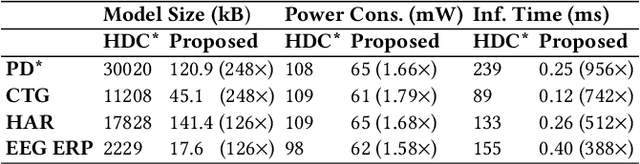
Abstract:Hyperdimensional computing (HDC) has emerged as a new light-weight learning algorithm with smaller computation and energy requirements compared to conventional techniques. In HDC, data points are represented by high-dimensional vectors (hypervectors), which are mapped to high-dimensional space (hyperspace). Typically, a large hypervector dimension ($\geq1000$) is required to achieve accuracies comparable to conventional alternatives. However, unnecessarily large hypervectors increase hardware and energy costs, which can undermine their benefits. This paper presents a technique to minimize the hypervector dimension while maintaining the accuracy and improving the robustness of the classifier. To this end, we formulate the hypervector design as a multi-objective optimization problem for the first time in the literature. The proposed approach decreases the hypervector dimension by more than $32\times$ while maintaining or increasing the accuracy achieved by conventional HDC. Experiments on a commercial hardware platform show that the proposed approach achieves more than one order of magnitude reduction in model size, inference time, and energy consumption. We also demonstrate the trade-off between accuracy and robustness to noise and provide Pareto front solutions as a design parameter in our hypervector design.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge