WHOMP: Optimizing Randomized Controlled Trials via Wasserstein Homogeneity

We investigate methods for partitioning datasets into subgroups that maximize diversity within each subgroup while minimizing dissimilarity across subgroups. We introduce a novel partitioning method called the $\textit{Wasserstein Homogeneity Partition}$ (WHOMP), which optimally minimizes type I and type II errors that often result from imbalanced group splitting or partitioning, commonly referred to as accidental bias, in comparative and controlled trials. We conduct an analytical comparison of WHOMP against existing partitioning methods, such as random subsampling, covariate-adaptive randomization, rerandomization, and anti-clustering, demonstrating its advantages. Moreover, we characterize the optimal solutions to the WHOMP problem and reveal an inherent trade-off between the stability of subgroup means and variances among these solutions. Based on our theoretical insights, we design algorithms that not only obtain these optimal solutions but also equip practitioners with tools to select the desired trade-off. Finally, we validate the effectiveness of WHOMP through numerical experiments, highlighting its superiority over traditional methods.

On the (In)Compatibility between Group Fairness and Individual Fairness

We study the compatibility between the optimal statistical parity solutions and individual fairness. While individual fairness seeks to treat similar individuals similarly, optimal statistical parity aims to provide similar treatment to individuals who share relative similarity within their respective sensitive groups. The two fairness perspectives, while both desirable from a fairness perspective, often come into conflict in applications. Our goal in this work is to analyze the existence of this conflict and its potential solution. In particular, we establish sufficient (sharp) conditions for the compatibility between the optimal (post-processing) statistical parity $L^2$ learning and the ($K$-Lipschitz or $(\epsilon,\delta)$) individual fairness requirements. Furthermore, when there exists a conflict between the two, we first relax the former to the Pareto frontier (or equivalently the optimal trade-off) between $L^2$ error and statistical disparity, and then analyze the compatibility between the frontier and the individual fairness requirements. Our analysis identifies regions along the Pareto frontier that satisfy individual fairness requirements. (Lastly, we provide individual fairness guarantees for the composition of a trained model and the optimal post-processing step so that one can determine the compatibility of the post-processed model.) This provides practitioners with a valuable approach to attain Pareto optimality for statistical parity while adhering to the constraints of individual fairness.

Fair Data Representation for Machine Learning at the Pareto Frontier

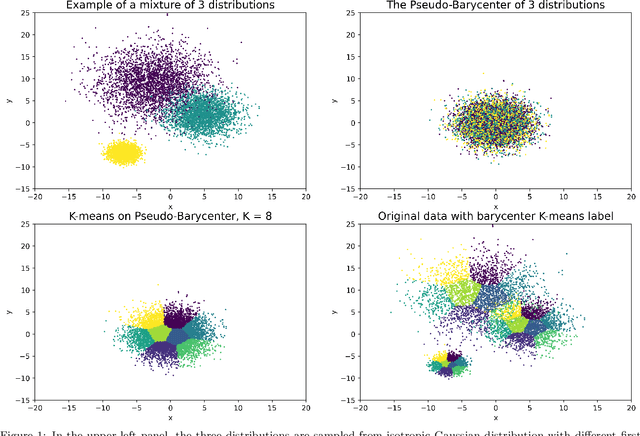
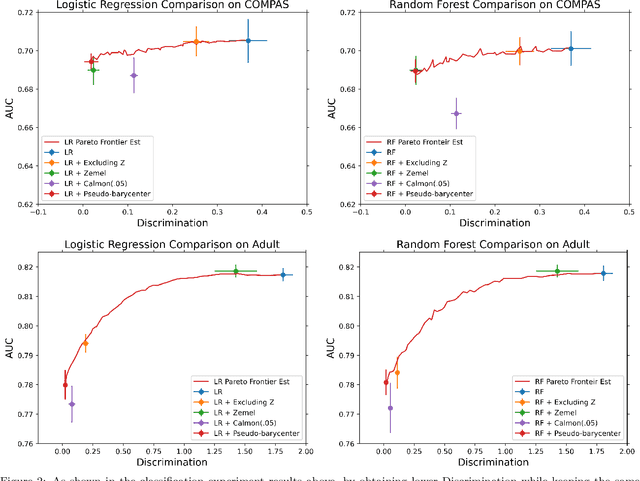
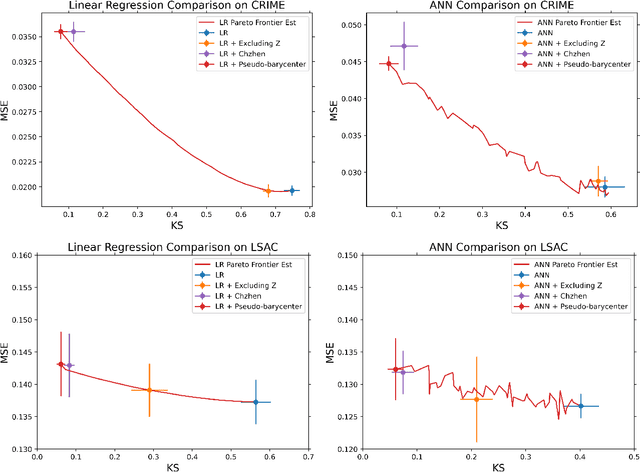
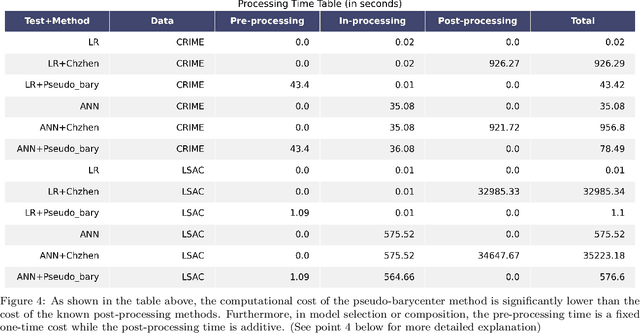
As machine learning powered decision making is playing an increasingly important role in our daily lives, it is imperative to strive for fairness of the underlying data processing and algorithms. We propose a pre-processing algorithm for fair data representation via which L2- objective supervised learning algorithms result in an estimation of the Pareto frontier between prediction error and statistical disparity. In particular, the present work applies the optimal positive definite affine transport maps to approach the post-processing Wasserstein barycenter characterization of the optimal fair L2-objective supervised learning via a pre-processing data deformation. We call the resulting data Wasserstein pseudo-barycenter. Furthermore, we show that the Wasserstein geodesics from the learning outcome marginals to the barycenter characterizes the Pareto frontier between L2-loss and total Wasserstein distance among learning outcome marginals. Thereby, an application of McCann interpolation generalizes the pseudo-barycenter to a family of data representations via which L2-objective supervised learning algorithms result in the Pareto frontier. Numerical simulations underscore the advantages of the proposed data representation: (1) the pre-processing step is compositive with arbitrary L2-objective supervised learning methods and unseen data; (2) the fair representation protects data privacy by preventing the training machine from direct or indirect access to the sensitive information of the data; (3) the optimal affine map results in efficient computation of fair supervised learning on high-dimensional data; (4) experimental results shed light on the fairness of L2-objective unsupervised learning via the proposed fair data representation.