Fair Data Representation for Machine Learning at the Pareto Frontier

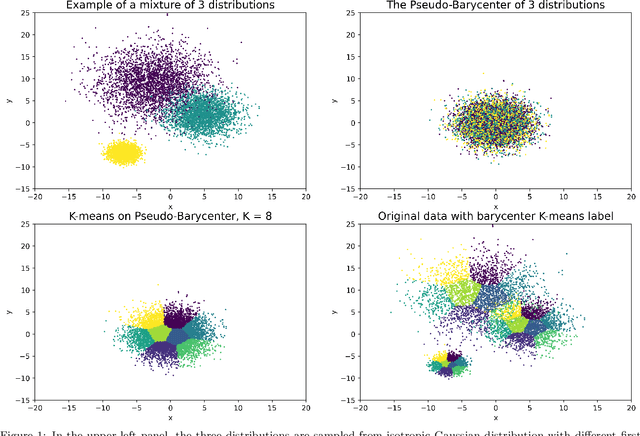
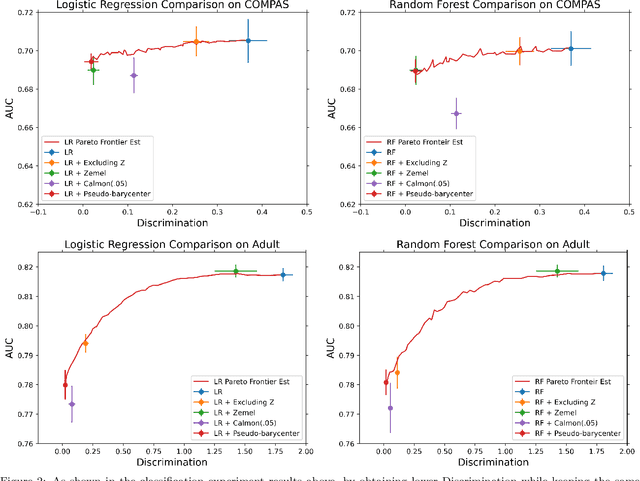
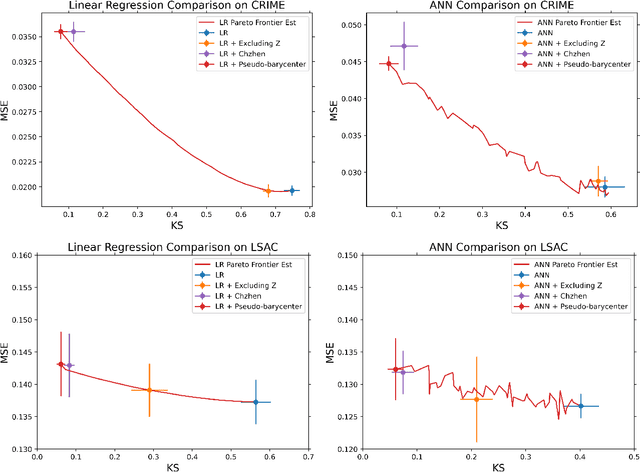
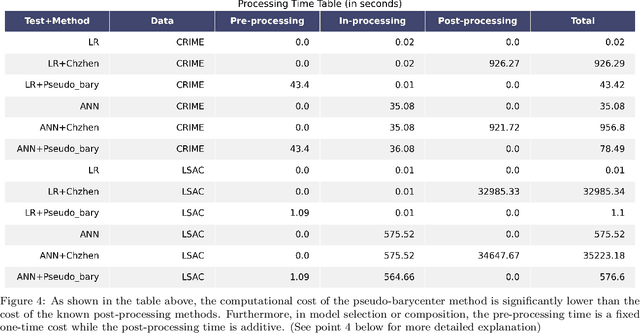
As machine learning powered decision making is playing an increasingly important role in our daily lives, it is imperative to strive for fairness of the underlying data processing and algorithms. We propose a pre-processing algorithm for fair data representation via which L2- objective supervised learning algorithms result in an estimation of the Pareto frontier between prediction error and statistical disparity. In particular, the present work applies the optimal positive definite affine transport maps to approach the post-processing Wasserstein barycenter characterization of the optimal fair L2-objective supervised learning via a pre-processing data deformation. We call the resulting data Wasserstein pseudo-barycenter. Furthermore, we show that the Wasserstein geodesics from the learning outcome marginals to the barycenter characterizes the Pareto frontier between L2-loss and total Wasserstein distance among learning outcome marginals. Thereby, an application of McCann interpolation generalizes the pseudo-barycenter to a family of data representations via which L2-objective supervised learning algorithms result in the Pareto frontier. Numerical simulations underscore the advantages of the proposed data representation: (1) the pre-processing step is compositive with arbitrary L2-objective supervised learning methods and unseen data; (2) the fair representation protects data privacy by preventing the training machine from direct or indirect access to the sensitive information of the data; (3) the optimal affine map results in efficient computation of fair supervised learning on high-dimensional data; (4) experimental results shed light on the fairness of L2-objective unsupervised learning via the proposed fair data representation.