WHOMP: Optimizing Randomized Controlled Trials via Wasserstein Homogeneity
Paper and Code
Sep 27, 2024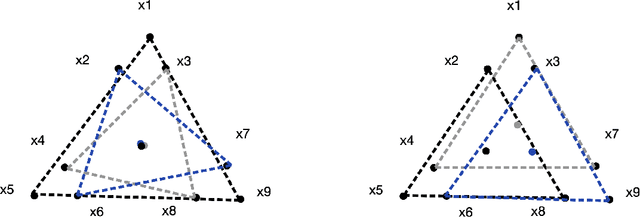
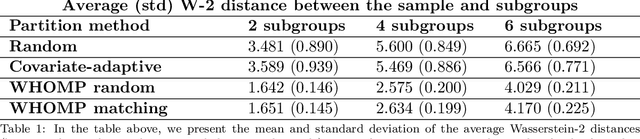
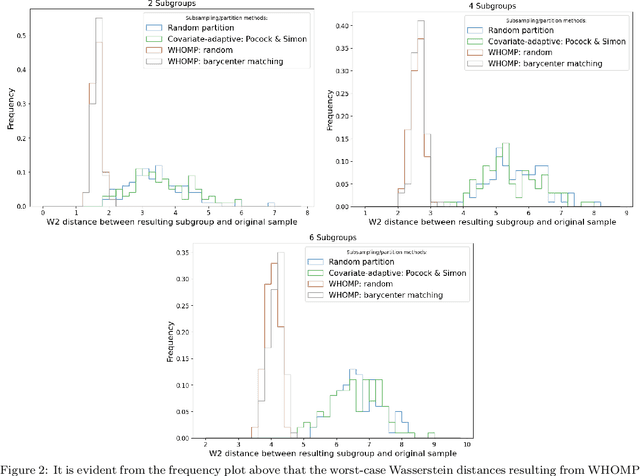

We investigate methods for partitioning datasets into subgroups that maximize diversity within each subgroup while minimizing dissimilarity across subgroups. We introduce a novel partitioning method called the $\textit{Wasserstein Homogeneity Partition}$ (WHOMP), which optimally minimizes type I and type II errors that often result from imbalanced group splitting or partitioning, commonly referred to as accidental bias, in comparative and controlled trials. We conduct an analytical comparison of WHOMP against existing partitioning methods, such as random subsampling, covariate-adaptive randomization, rerandomization, and anti-clustering, demonstrating its advantages. Moreover, we characterize the optimal solutions to the WHOMP problem and reveal an inherent trade-off between the stability of subgroup means and variances among these solutions. Based on our theoretical insights, we design algorithms that not only obtain these optimal solutions but also equip practitioners with tools to select the desired trade-off. Finally, we validate the effectiveness of WHOMP through numerical experiments, highlighting its superiority over traditional methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge