Kalman meets Bellman: Improving Policy Evaluation through Value Tracking

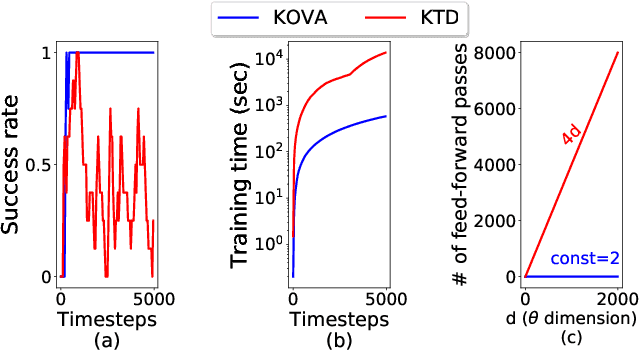
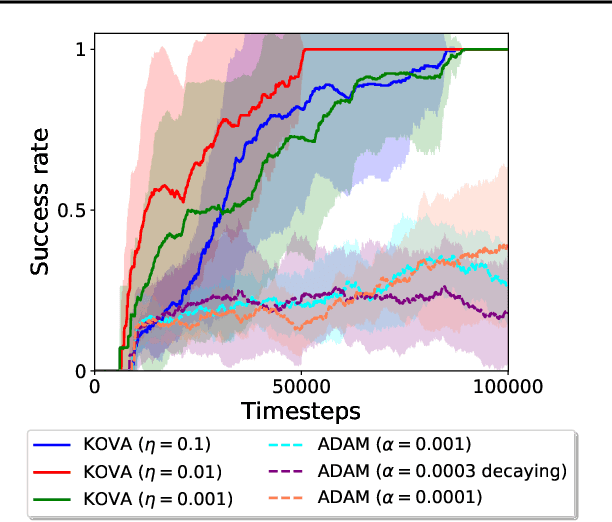
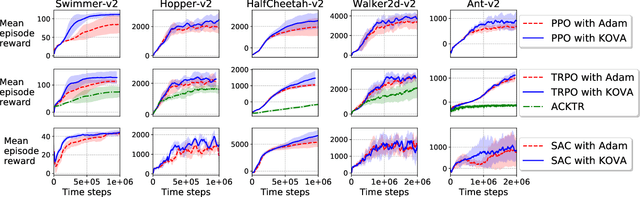
Policy evaluation is a key process in Reinforcement Learning (RL). It assesses a given policy by estimating the corresponding value function. When using parameterized value functions, common approaches minimize the sum of squared Bellman temporal-difference errors and receive a point-estimate for the parameters. Kalman-based and Gaussian-processes based frameworks were suggested to evaluate the policy by treating the value as a random variable. These frameworks can learn uncertainties over the value parameters and exploit them for policy exploration. When adopting these frameworks to solve deep RL tasks, several limitations are revealed: excessive computations in each optimization step, difficulty with handling batches of samples which slows training and the effect of memory in stochastic environments which prevents off-policy learning. In this work, we discuss these limitations and propose to overcome them by an alternative general framework, based on the extended Kalman filter. We devise an optimization method, called Kalman Optimization for Value Approximation (KOVA) that can be incorporated as a policy evaluation component in policy optimization algorithms. KOVA minimizes a regularized objective function that concerns both parameter and noisy return uncertainties. We analyze the properties of KOVA and present its performance on deep RL control tasks.

Trust Region Value Optimization using Kalman Filtering

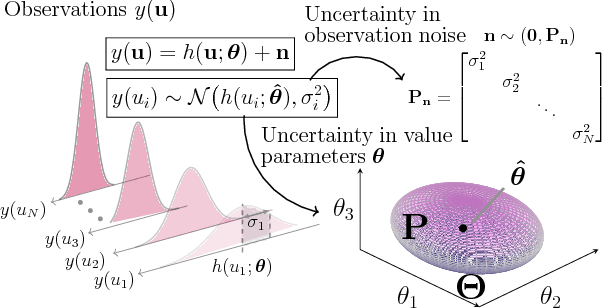
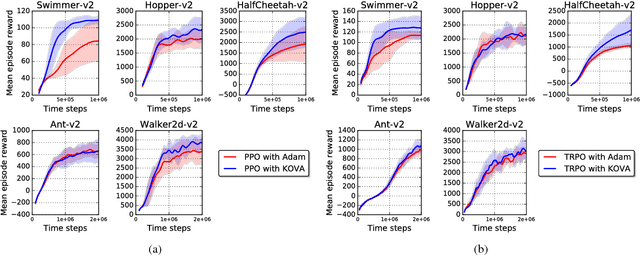
Policy evaluation is a key process in reinforcement learning. It assesses a given policy using estimation of the corresponding value function. When using a parameterized function to approximate the value, it is common to optimize the set of parameters by minimizing the sum of squared Bellman Temporal Differences errors. However, this approach ignores certain distributional properties of both the errors and value parameters. Taking these distributions into account in the optimization process can provide useful information on the amount of confidence in value estimation. In this work we propose to optimize the value by minimizing a regularized objective function which forms a trust region over its parameters. We present a novel optimization method, the Kalman Optimization for Value Approximation (KOVA), based on the Extended Kalman Filter. KOVA minimizes the regularized objective function by adopting a Bayesian perspective over both the value parameters and noisy observed returns. This distributional property provides information on parameter uncertainty in addition to value estimates. We provide theoretical results of our approach and analyze the performance of our proposed optimizer on domains with large state and action spaces.

Deep Robust Kalman Filter

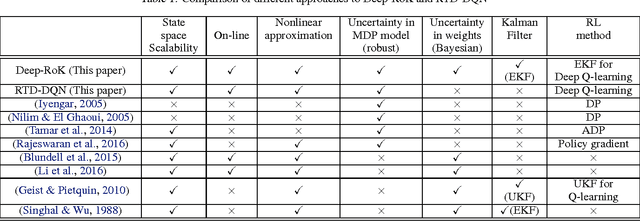
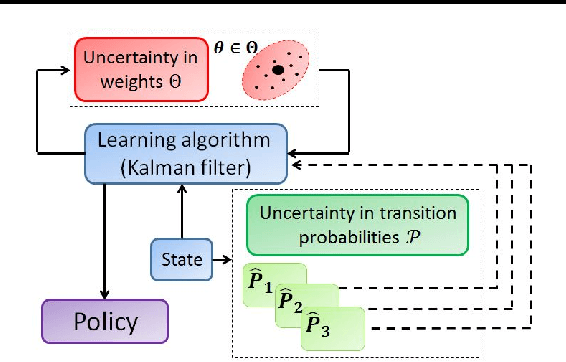
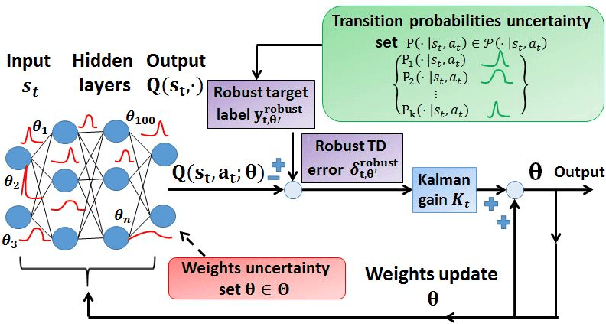
A Robust Markov Decision Process (RMDP) is a sequential decision making model that accounts for uncertainty in the parameters of dynamic systems. This uncertainty introduces difficulties in learning an optimal policy, especially for environments with large state spaces. We propose two algorithms, RTD-DQN and Deep-RoK, for solving large-scale RMDPs using nonlinear approximation schemes such as deep neural networks. The RTD-DQN algorithm incorporates the robust Bellman temporal difference error into a robust loss function, yielding robust policies for the agent. The Deep-RoK algorithm is a robust Bayesian method, based on the Extended Kalman Filter (EKF), that accounts for both the uncertainty in the weights of the approximated value function and the uncertainty in the transition probabilities, improving the robustness of the agent. We provide theoretical results for our approach and test the proposed algorithms on a continuous state domain.