Deep Robust Kalman Filter
Paper and Code
Mar 07, 2017
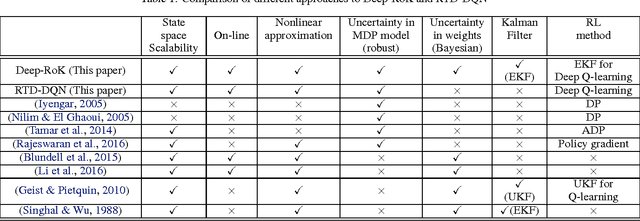
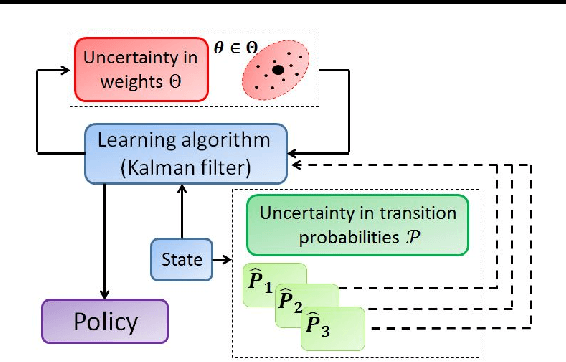
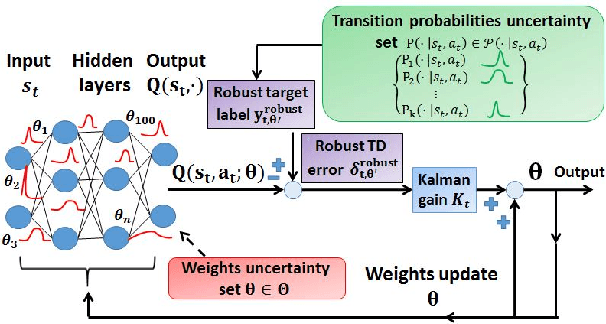
A Robust Markov Decision Process (RMDP) is a sequential decision making model that accounts for uncertainty in the parameters of dynamic systems. This uncertainty introduces difficulties in learning an optimal policy, especially for environments with large state spaces. We propose two algorithms, RTD-DQN and Deep-RoK, for solving large-scale RMDPs using nonlinear approximation schemes such as deep neural networks. The RTD-DQN algorithm incorporates the robust Bellman temporal difference error into a robust loss function, yielding robust policies for the agent. The Deep-RoK algorithm is a robust Bayesian method, based on the Extended Kalman Filter (EKF), that accounts for both the uncertainty in the weights of the approximated value function and the uncertainty in the transition probabilities, improving the robustness of the agent. We provide theoretical results for our approach and test the proposed algorithms on a continuous state domain.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge