Kalman meets Bellman: Improving Policy Evaluation through Value Tracking
Paper and Code
Feb 17, 2020
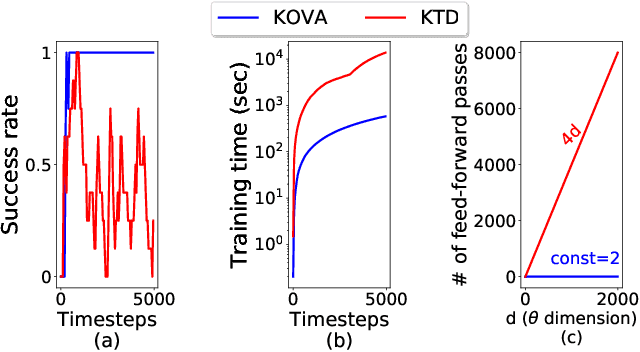
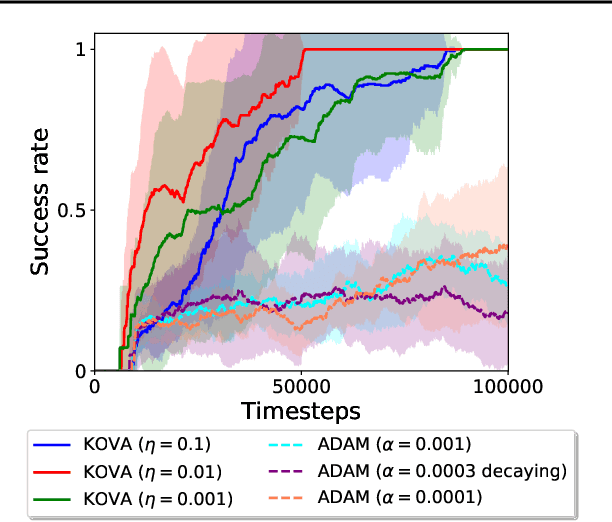
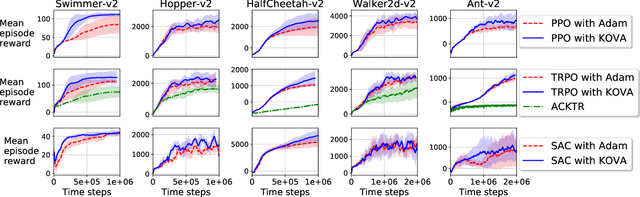
Policy evaluation is a key process in Reinforcement Learning (RL). It assesses a given policy by estimating the corresponding value function. When using parameterized value functions, common approaches minimize the sum of squared Bellman temporal-difference errors and receive a point-estimate for the parameters. Kalman-based and Gaussian-processes based frameworks were suggested to evaluate the policy by treating the value as a random variable. These frameworks can learn uncertainties over the value parameters and exploit them for policy exploration. When adopting these frameworks to solve deep RL tasks, several limitations are revealed: excessive computations in each optimization step, difficulty with handling batches of samples which slows training and the effect of memory in stochastic environments which prevents off-policy learning. In this work, we discuss these limitations and propose to overcome them by an alternative general framework, based on the extended Kalman filter. We devise an optimization method, called Kalman Optimization for Value Approximation (KOVA) that can be incorporated as a policy evaluation component in policy optimization algorithms. KOVA minimizes a regularized objective function that concerns both parameter and noisy return uncertainties. We analyze the properties of KOVA and present its performance on deep RL control tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge