Trust Region Value Optimization using Kalman Filtering
Paper and Code
Jan 23, 2019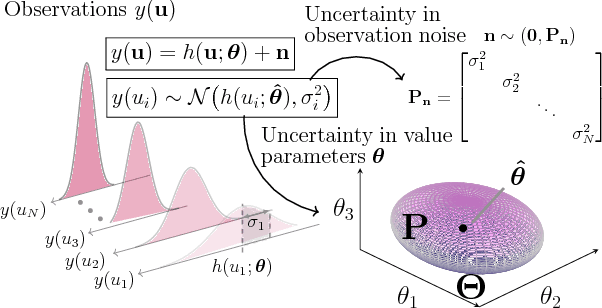


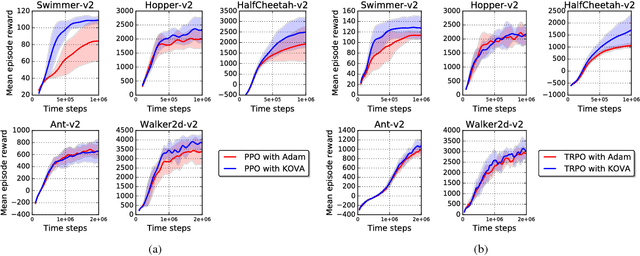
Policy evaluation is a key process in reinforcement learning. It assesses a given policy using estimation of the corresponding value function. When using a parameterized function to approximate the value, it is common to optimize the set of parameters by minimizing the sum of squared Bellman Temporal Differences errors. However, this approach ignores certain distributional properties of both the errors and value parameters. Taking these distributions into account in the optimization process can provide useful information on the amount of confidence in value estimation. In this work we propose to optimize the value by minimizing a regularized objective function which forms a trust region over its parameters. We present a novel optimization method, the Kalman Optimization for Value Approximation (KOVA), based on the Extended Kalman Filter. KOVA minimizes the regularized objective function by adopting a Bayesian perspective over both the value parameters and noisy observed returns. This distributional property provides information on parameter uncertainty in addition to value estimates. We provide theoretical results of our approach and analyze the performance of our proposed optimizer on domains with large state and action spaces.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge