Geometry-Preserving Neural Architectures on Manifolds with Boundary

Preserving geometric structure is important in learning. We propose a unified class of geometry-aware architectures that interleave geometric updates between layers, where both projection layers and intrinsic exponential map updates arise as discretizations of projected dynamical systems on manifolds (with or without boundary). Within this framework, we establish universal approximation results for constrained neural ODEs. We also analyze architectures that enforce geometry only at the output, proving a separate universal approximation property that enables direct comparison to interleaved designs. When the constraint set is unknown, we learn projections via small-time heat-kernel limits, showing diffusion/flow-matching can be used as data-based projections. Experiments on dynamics over S^2 and SO(3), and diffusion on S^{d-1}-valued features demonstrate exact feasibility for analytic updates and strong performance for learned projections

Mean-Field Controllability and Decentralized Stabilization of Markov Chains, Part II: Asymptotic Controllability and Polynomial Feedbacks

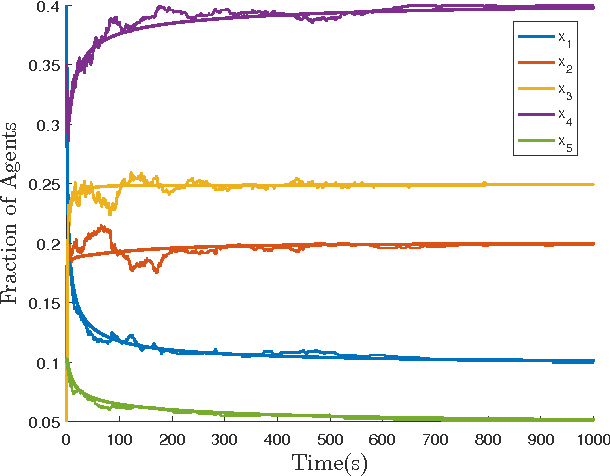
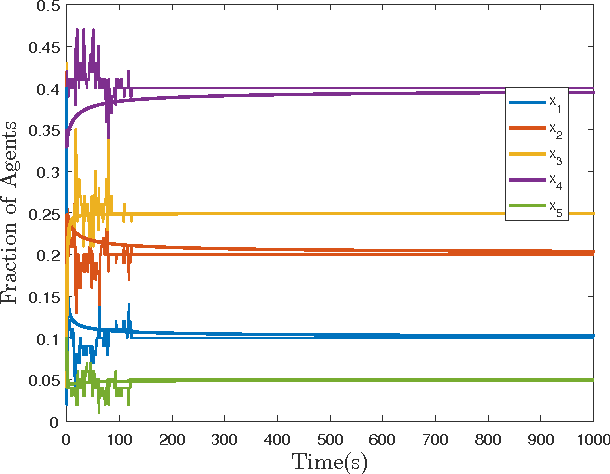
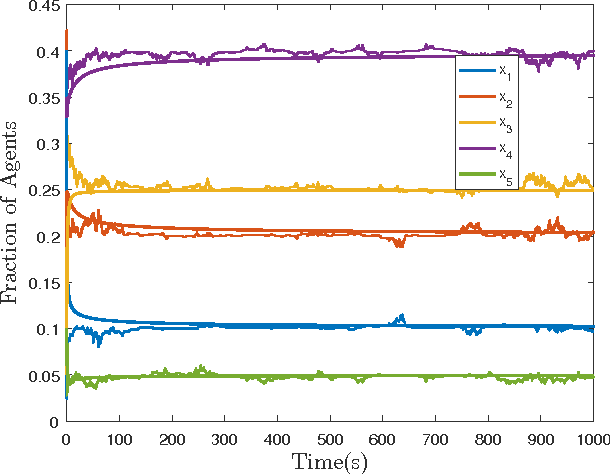
This paper, the second of a two-part series, presents a method for mean-field feedback stabilization of a swarm of agents on a finite state space whose time evolution is modeled as a continuous time Markov chain (CTMC). The resulting (mean-field) control problem is that of controlling a nonlinear system with desired global stability properties. We first prove that any probability distribution with a strongly connected support can be stabilized using time-invariant inputs. Secondly, we show the asymptotic controllability of all possible probability distributions, including distributions that assign zero density to some states and which do not necessarily have a strongly connected support. Lastly, we demonstrate that there always exists a globally asymptotically stabilizing decentralized density feedback law with the additional property that the control inputs are zero at equilibrium, whenever the graph is strongly connected and bidirected. Then the problem of synthesizing closed-loop polynomial feedback is framed as a optimization problem using state-of-the-art sum-of-squares optimization tools. The optimization problem searches for polynomial feedback laws that make the candidate Lyapunov function a stability certificate for the resulting closed-loop system. Our methodology is tested for two cases on a five vertex graph, and the stabilization properties of the constructed control laws are validated with numerical simulations of the corresponding system of ordinary differential equations.