Likelihood estimation of sparse topic distributions in topic models and its applications to Wasserstein document distance calculations

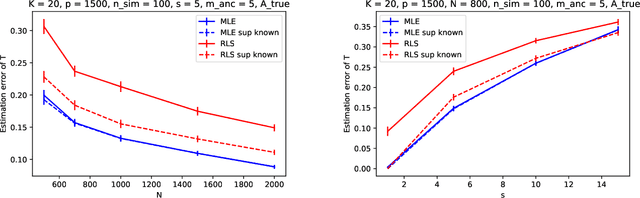
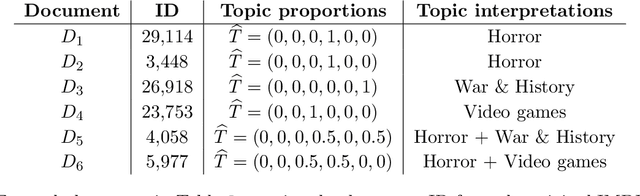
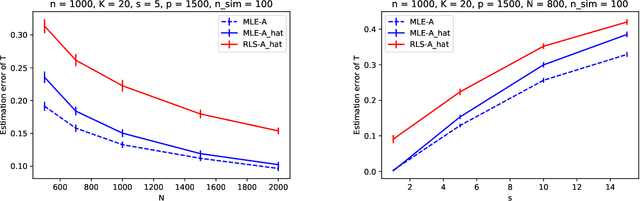
This paper studies the estimation of high-dimensional, discrete, possibly sparse, mixture models in topic models. The data consists of observed multinomial counts of $p$ words across $n$ independent documents. In topic models, the $p\times n$ expected word frequency matrix is assumed to be factorized as a $p\times K$ word-topic matrix $A$ and a $K\times n$ topic-document matrix $T$. Since columns of both matrices represent conditional probabilities belonging to probability simplices, columns of $A$ are viewed as $p$-dimensional mixture components that are common to all documents while columns of $T$ are viewed as the $K$-dimensional mixture weights that are document specific and are allowed to be sparse. The main interest is to provide sharp, finite sample, $\ell_1$-norm convergence rates for estimators of the mixture weights $T$ when $A$ is either known or unknown. For known $A$, we suggest MLE estimation of $T$. Our non-standard analysis of the MLE not only establishes its $\ell_1$ convergence rate, but reveals a remarkable property: the MLE, with no extra regularization, can be exactly sparse and contain the true zero pattern of $T$. We further show that the MLE is both minimax optimal and adaptive to the unknown sparsity in a large class of sparse topic distributions. When $A$ is unknown, we estimate $T$ by optimizing the likelihood function corresponding to a plug in, generic, estimator $\hat{A}$ of $A$. For any estimator $\hat{A}$ that satisfies carefully detailed conditions for proximity to $A$, the resulting estimator of $T$ is shown to retain the properties established for the MLE. The ambient dimensions $K$ and $p$ are allowed to grow with the sample sizes. Our application is to the estimation of 1-Wasserstein distances between document generating distributions. We propose, estimate and analyze new 1-Wasserstein distances between two probabilistic document representations.

Prediction in latent factor regression: Adaptive PCR and beyond

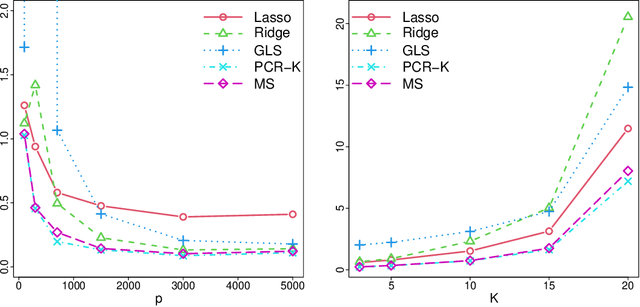
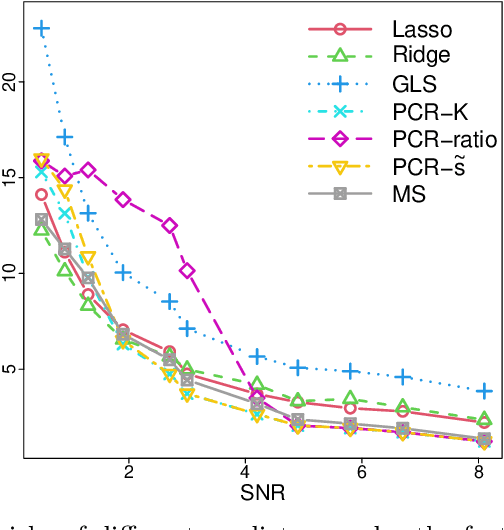
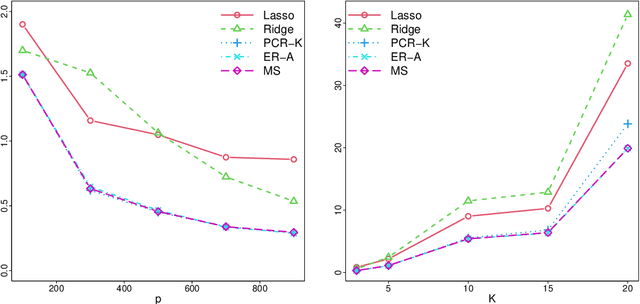
This work is devoted to the finite sample prediction risk analysis of a class of linear predictors of a response $Y\in \mathbb{R}$ from a high-dimensional random vector $X\in \mathbb{R}^p$ when $(X,Y)$ follows a latent factor regression model generated by a unobservable latent vector $Z$ of dimension less than $p$. Our primary contribution is in establishing finite sample risk bounds for prediction with the ubiquitous Principal Component Regression (PCR) method, under the factor regression model, with the number of principal components adaptively selected from the data---a form of theoretical guarantee that is surprisingly lacking from the PCR literature. To accomplish this, we prove a master theorem that establishes a risk bound for a large class of predictors, including the PCR predictor as a special case. This approach has the benefit of providing a unified framework for the analysis of a wide range of linear prediction methods, under the factor regression setting. In particular, we use our main theorem to recover known risk bounds for the minimum-norm interpolating predictor, which has received renewed attention in the past two years, and a prediction method tailored to a subclass of factor regression models with identifiable parameters. This model-tailored method can be interpreted as prediction via clusters with latent centers. To address the problem of selecting among a set of candidate predictors, we analyze a simple model selection procedure based on data-splitting, providing an oracle inequality under the factor model to prove that the performance of the selected predictor is close to the optimal candidate. We conclude with a detailed simulation study to support and complement our theoretical results.

Interpolation under latent factor regression models

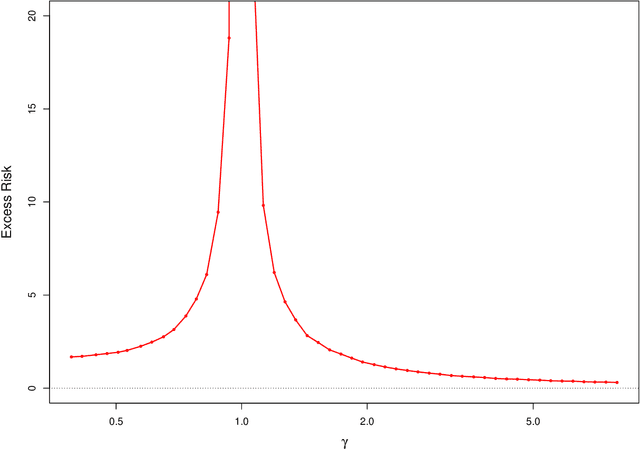
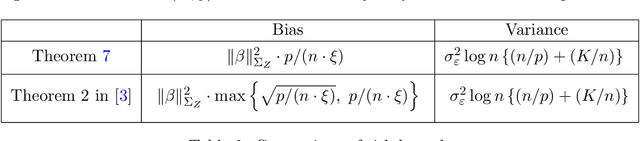
This work studies finite-sample properties of the risk of the minimum-norm interpolating predictor in high-dimensional regression models. If the effective rank of the covariance matrix $\Sigma$ of the $p$ regression features is much larger than the sample size $n$, we show that the min-norm interpolating predictor is not desirable, as its risk approaches the risk of trivially predicting the response by $0$. However, our detailed finite sample analysis reveals, surprisingly, that this behavior is not present when the regression response and the features are jointly low-dimensional, and follow a widely used factor regression model. Within this popular model class, and when the effective rank of $\Sigma$ is smaller than $n$, while still allowing for $p \gg n$, both the bias and the variance terms of the excess risk can be controlled, and the risk of the minimum-norm interpolating predictor approaches optimal benchmarks. Moreover, through a detailed analysis of the bias term, we exhibit model classes under which our upper bound on the excess risk approaches zero, while the corresponding upper bound in the recent work arXiv:1906.11300v3 diverges. Furthermore, we show that minimum-norm interpolating predictors analyzed under factor regression models, despite being model-agnostic, can have similar risk to model-assisted predictors based on principal components regression, in the high-dimensional regime.