Likelihood estimation of sparse topic distributions in topic models and its applications to Wasserstein document distance calculations
Paper and Code
Jul 12, 2021
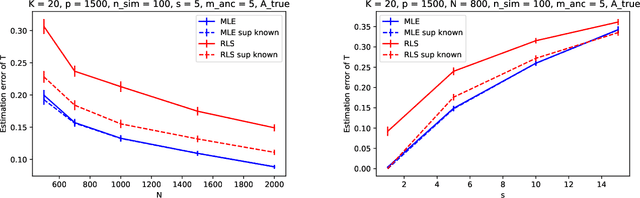
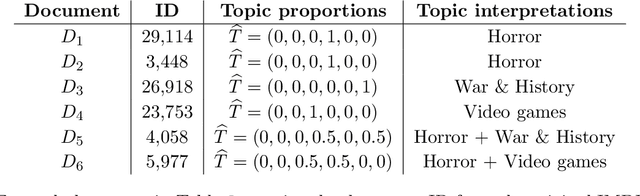
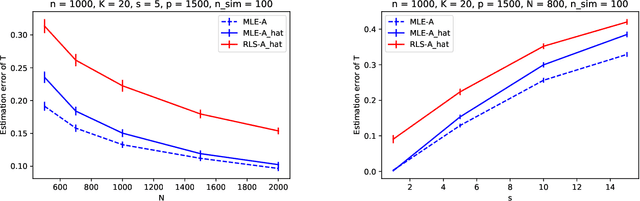
This paper studies the estimation of high-dimensional, discrete, possibly sparse, mixture models in topic models. The data consists of observed multinomial counts of $p$ words across $n$ independent documents. In topic models, the $p\times n$ expected word frequency matrix is assumed to be factorized as a $p\times K$ word-topic matrix $A$ and a $K\times n$ topic-document matrix $T$. Since columns of both matrices represent conditional probabilities belonging to probability simplices, columns of $A$ are viewed as $p$-dimensional mixture components that are common to all documents while columns of $T$ are viewed as the $K$-dimensional mixture weights that are document specific and are allowed to be sparse. The main interest is to provide sharp, finite sample, $\ell_1$-norm convergence rates for estimators of the mixture weights $T$ when $A$ is either known or unknown. For known $A$, we suggest MLE estimation of $T$. Our non-standard analysis of the MLE not only establishes its $\ell_1$ convergence rate, but reveals a remarkable property: the MLE, with no extra regularization, can be exactly sparse and contain the true zero pattern of $T$. We further show that the MLE is both minimax optimal and adaptive to the unknown sparsity in a large class of sparse topic distributions. When $A$ is unknown, we estimate $T$ by optimizing the likelihood function corresponding to a plug in, generic, estimator $\hat{A}$ of $A$. For any estimator $\hat{A}$ that satisfies carefully detailed conditions for proximity to $A$, the resulting estimator of $T$ is shown to retain the properties established for the MLE. The ambient dimensions $K$ and $p$ are allowed to grow with the sample sizes. Our application is to the estimation of 1-Wasserstein distances between document generating distributions. We propose, estimate and analyze new 1-Wasserstein distances between two probabilistic document representations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge