Interpolation under latent factor regression models

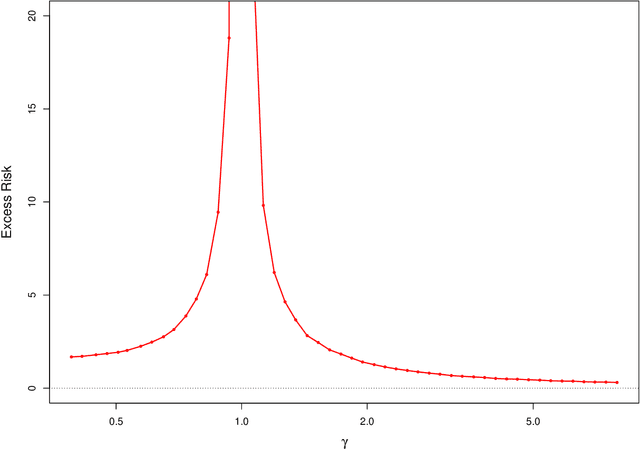
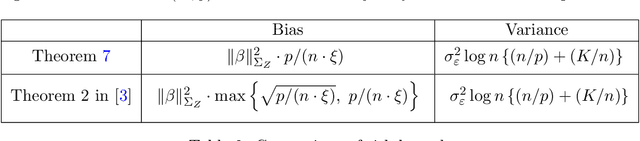
This work studies finite-sample properties of the risk of the minimum-norm interpolating predictor in high-dimensional regression models. If the effective rank of the covariance matrix $\Sigma$ of the $p$ regression features is much larger than the sample size $n$, we show that the min-norm interpolating predictor is not desirable, as its risk approaches the risk of trivially predicting the response by $0$. However, our detailed finite sample analysis reveals, surprisingly, that this behavior is not present when the regression response and the features are jointly low-dimensional, and follow a widely used factor regression model. Within this popular model class, and when the effective rank of $\Sigma$ is smaller than $n$, while still allowing for $p \gg n$, both the bias and the variance terms of the excess risk can be controlled, and the risk of the minimum-norm interpolating predictor approaches optimal benchmarks. Moreover, through a detailed analysis of the bias term, we exhibit model classes under which our upper bound on the excess risk approaches zero, while the corresponding upper bound in the recent work arXiv:1906.11300v3 diverges. Furthermore, we show that minimum-norm interpolating predictors analyzed under factor regression models, despite being model-agnostic, can have similar risk to model-assisted predictors based on principal components regression, in the high-dimensional regime.