Sergey Chervontsev
Regression Prior Networks
Jun 20, 2020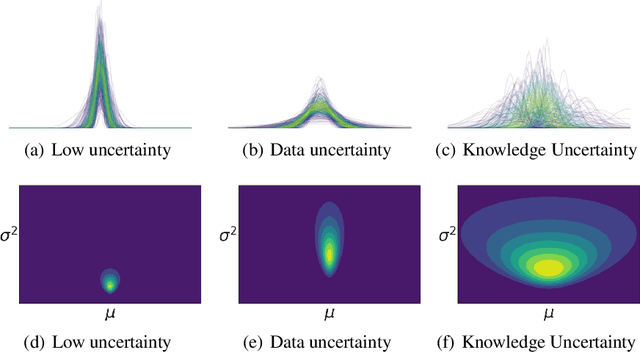

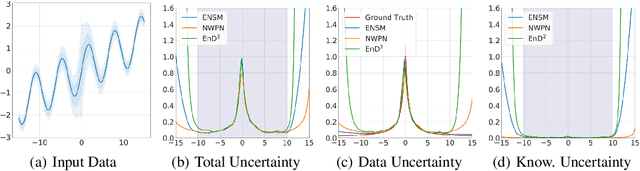
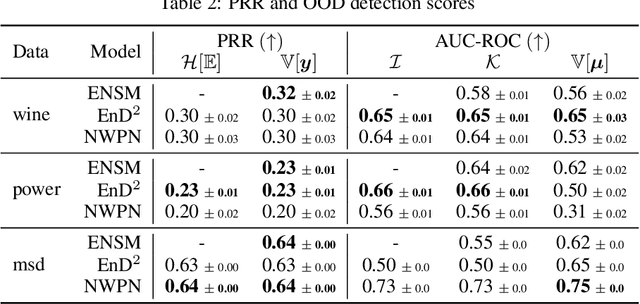
Abstract:Prior Networks are a recently developed class of models which yield interpretable measures of uncertainty and have been shown to outperform state-of-the-art ensemble approaches on a range of tasks. They can also be used to distill an ensemble of models via Ensemble Distribution Distillation (EnD$^2$), such that its accuracy, calibration and uncertainty estimates are retained within a single model. However, Prior Networks have so far been developed only for classification tasks. This work extends Prior Networks and EnD$^2$ to regression tasks by considering the Normal-Wishart distribution. The properties of Regression Prior Networks are demonstrated on synthetic data, selected UCI datasets and a monocular depth estimation task, where they yield performance competitive with ensemble approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge