Serena Hacker
Preventing Arbitrarily High Confidence on Far-Away Data in Point-Estimated Discriminative Neural Networks
Nov 07, 2023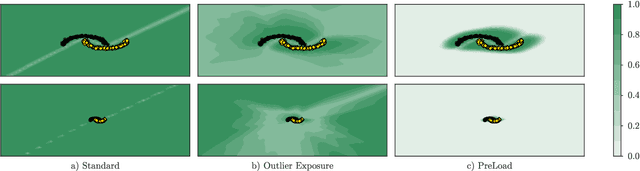
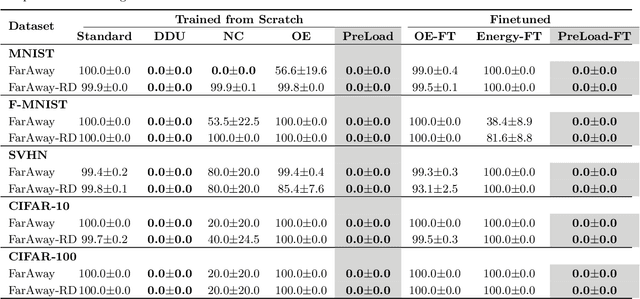

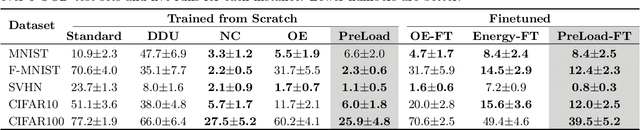
Abstract:Discriminatively trained, deterministic neural networks are the de facto choice for classification problems. However, even though they achieve state-of-the-art results on in-domain test sets, they tend to be overconfident on out-of-distribution (OOD) data. For instance, ReLU networks -- a popular class of neural network architectures -- have been shown to almost always yield high confidence predictions when the test data are far away from the training set, even when they are trained with OOD data. We overcome this problem by adding a term to the output of the neural network that corresponds to the logit of an extra class, that we design to dominate the logits of the original classes as we move away from the training data.This technique provably prevents arbitrarily high confidence on far-away test data while maintaining a simple discriminative point-estimate training. Evaluation on various benchmarks demonstrates strong performance against competitive baselines on both far-away and realistic OOD data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge