Get our free extension to see links to code for papers anywhere online!Free add-on: code for papers everywhere!Free add-on: See code for papers anywhere!
Sang-Won Park
Correspondence between neuroevolution and gradient descent
Aug 15, 2020Figures and Tables: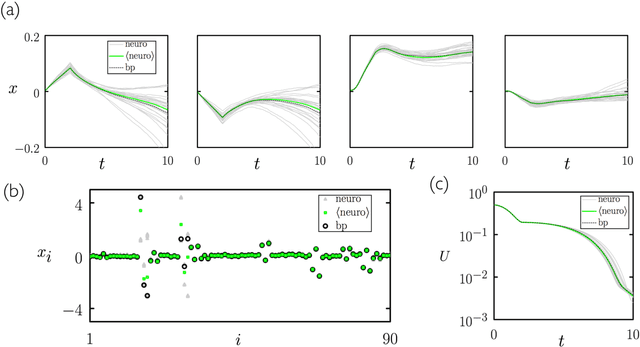
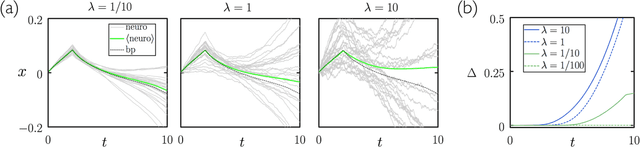
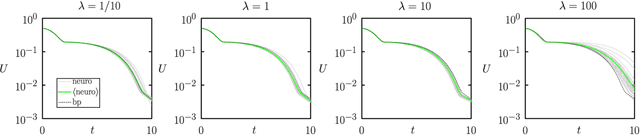



Abstract:We show analytically that training a neural network by stochastic mutation or "neuroevolution" of its weights is equivalent, in the limit of small mutations, to gradient descent on the loss function in the presence of Gaussian white noise. Averaged over independent realizations of the learning process, neuroevolution is equivalent to gradient descent on the loss function. We use numerical simulation to show that this correspondence can be observed for finite mutations. Our results provide a connection between two distinct types of neural-network training, and provide justification for the empirical success of neuroevolution.
Via
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge