The Partial Response Network

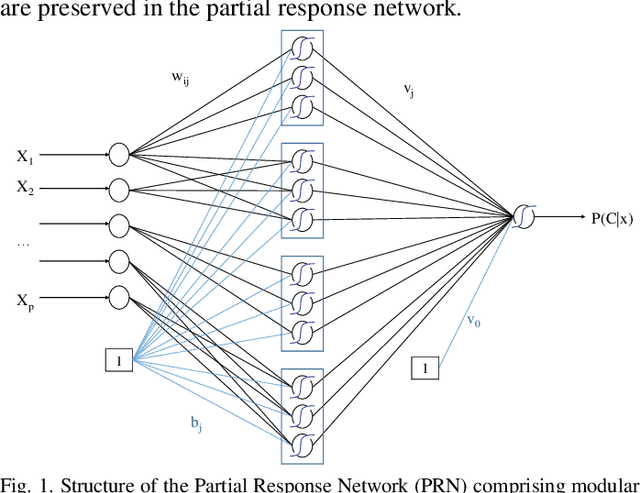
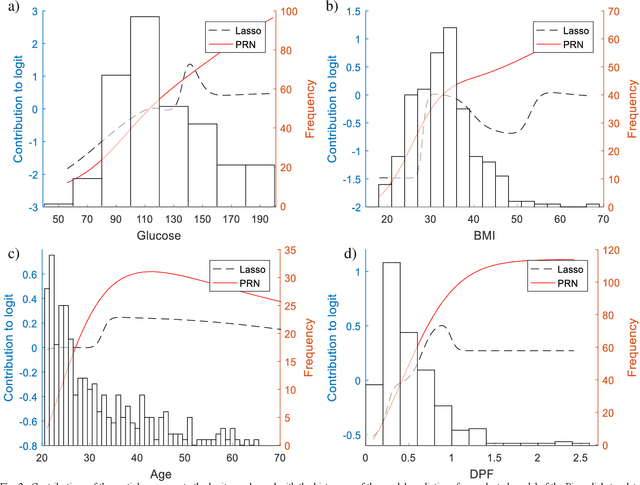
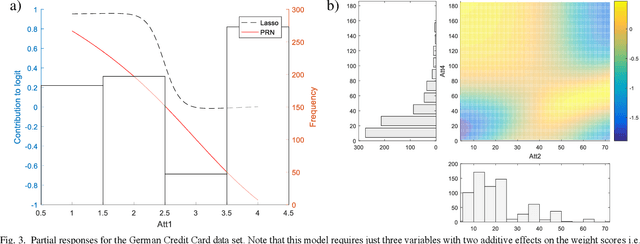
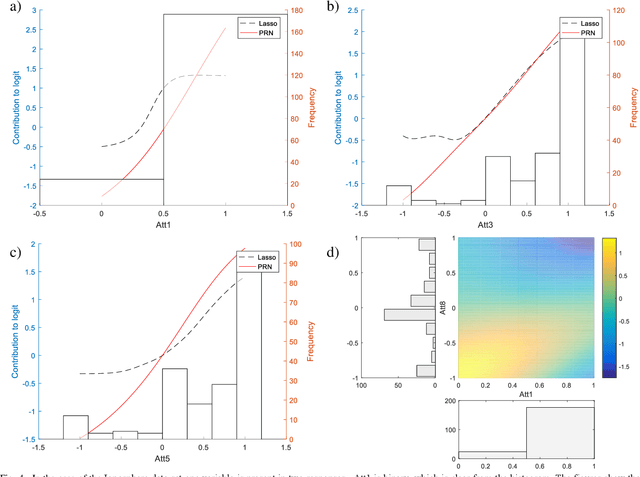
We propose a method to open the black box of the Multi-Layer Perceptron by inferring from it a simpler and generally more accurate general additive model. The resulting model comprises non-linear univariate and bivariate partial responses derived from the original Multi-Layer Perceptron. The responses are combined using the Lasso and further optimised within a modular structure. The approach is generic and provides a constructive framework to simplify and explain the Multi-Layer Perceptron for any data set, opening the door for validation against prior knowledge. Experimental results on benchmarking datasets indicate that the partial responses are intuitive to interpret and the Area Under the Curve is competitive with Gradient Boosting, Support Vector Machines and Random Forests. The performance improvement compared with a fully connected Multi-Layer Perceptron is attributed to reduced confounding in the second stage of optimisation of the weights. The main limitation of the method is that it explicitly models only up to pairwise interactions. For many practical applications this will be optimal, but where that is not the case then this will be indicated by the performance difference compared to the original model. The streamlined model simultaneously interprets and optimises this frequently used flexible model.

A Probabilistic framework for Quantum Clustering

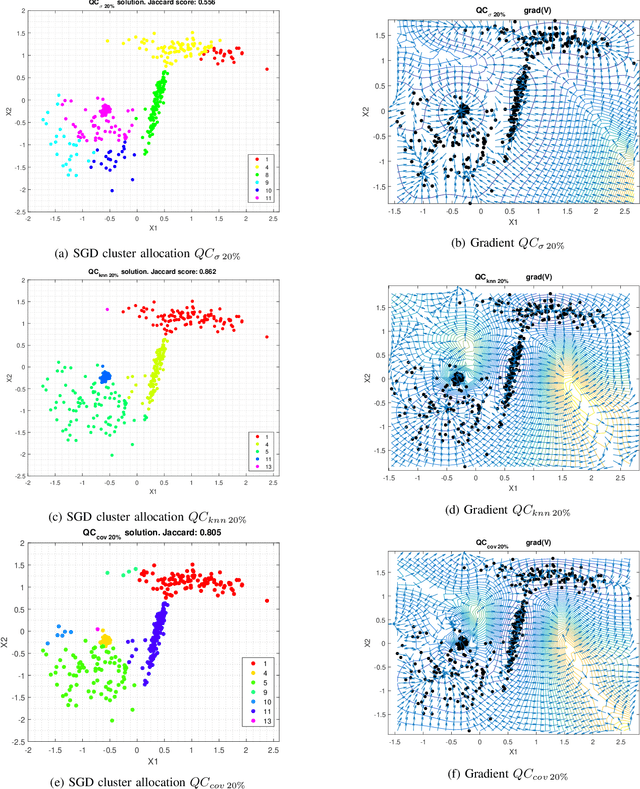
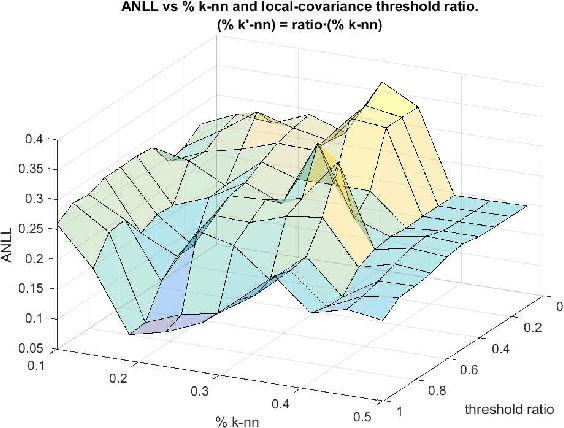
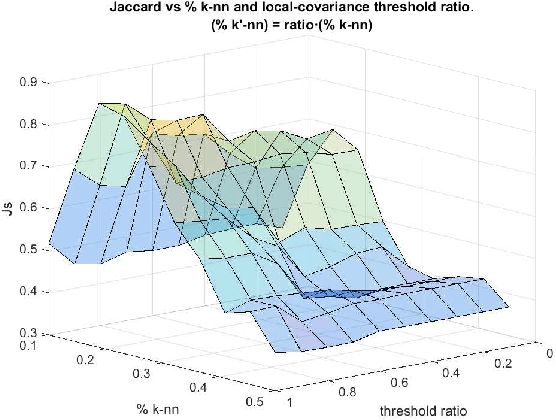
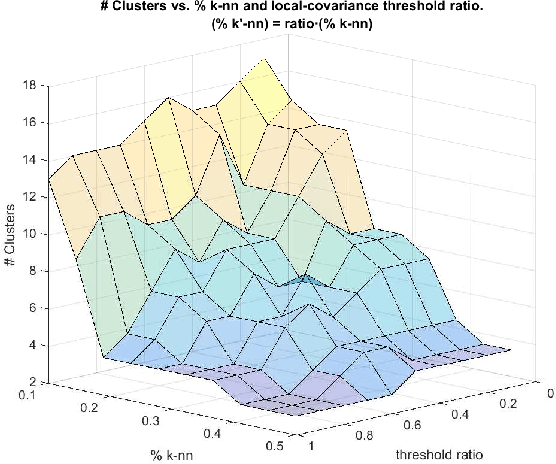
Quantum Clustering is a powerful method to detect clusters in data with mixed density. However, it is very sensitive to a length parameter that is inherent to the Schr\"odinger equation. In addition, linking data points into clusters requires local estimates of covariance that are also controlled by length parameters. This raises the question of how to adjust the control parameters of the Schr\"odinger equation for optimal clustering. We propose a probabilistic framework that provides an objective function for the goodness-of-fit to the data, enabling the control parameters to be optimised within a Bayesian framework. This naturally yields probabilities of cluster membership and data partitions with specific numbers of clusters. The proposed framework is tested on real and synthetic data sets, assessing its validity by measuring concordance with known data structure by means of the Jaccard score (JS). This work also proposes an objective way to measure performance in unsupervised learning that correlates very well with JS.