Ian H. Jarman
A Probabilistic framework for Quantum Clustering
Feb 14, 2019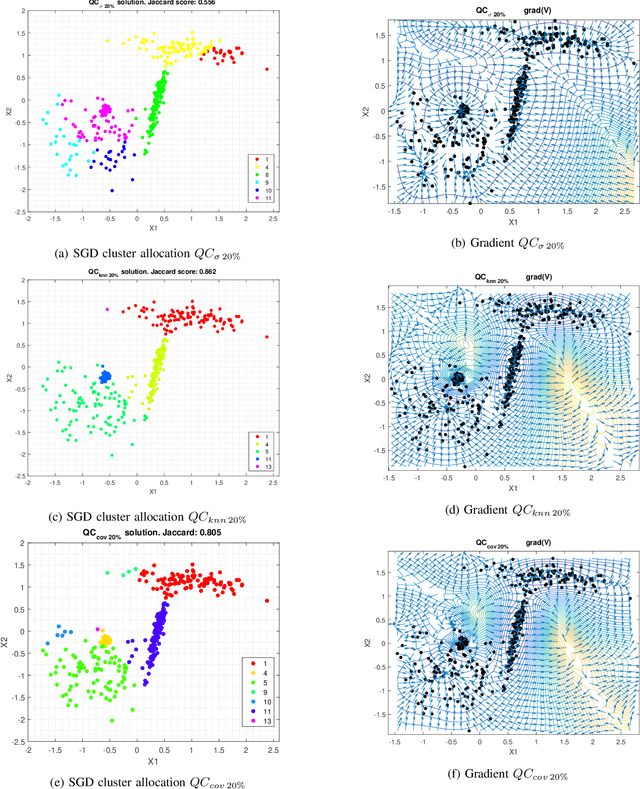
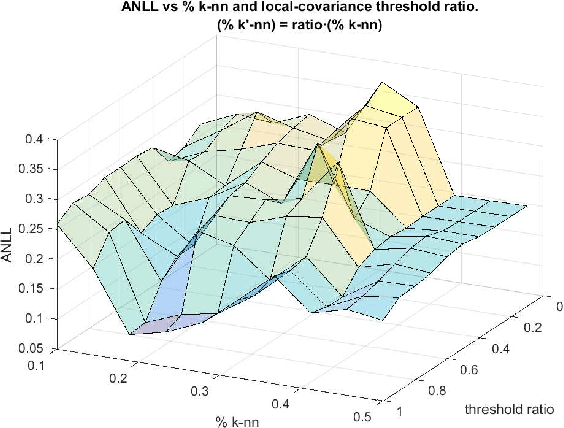
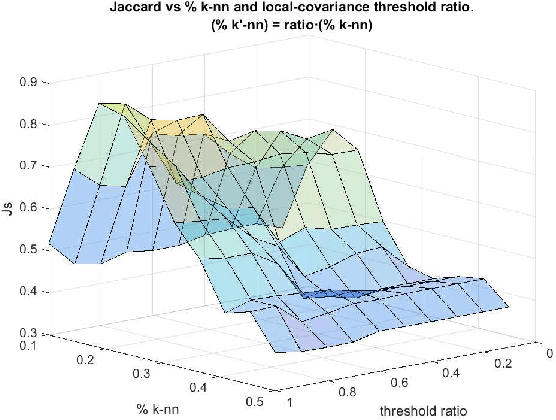
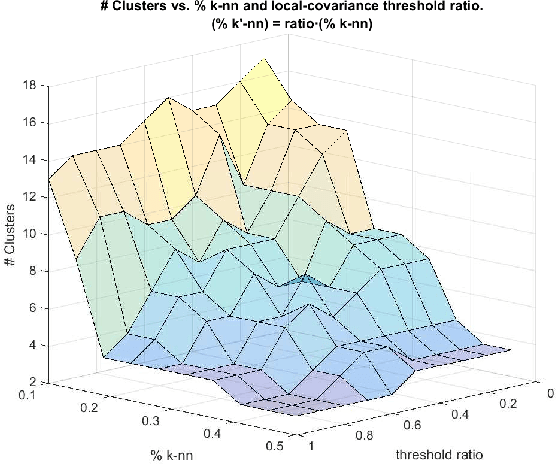
Abstract:Quantum Clustering is a powerful method to detect clusters in data with mixed density. However, it is very sensitive to a length parameter that is inherent to the Schr\"odinger equation. In addition, linking data points into clusters requires local estimates of covariance that are also controlled by length parameters. This raises the question of how to adjust the control parameters of the Schr\"odinger equation for optimal clustering. We propose a probabilistic framework that provides an objective function for the goodness-of-fit to the data, enabling the control parameters to be optimised within a Bayesian framework. This naturally yields probabilities of cluster membership and data partitions with specific numbers of clusters. The proposed framework is tested on real and synthetic data sets, assessing its validity by measuring concordance with known data structure by means of the Jaccard score (JS). This work also proposes an objective way to measure performance in unsupervised learning that correlates very well with JS.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge