A-MHA*: Anytime Multi-Heuristic A*

Designing good heuristic functions for graph search requires adequate domain knowledge. It is often easy to design heuristics that perform well and correlate with the underlying true cost-to-go values in certain parts of the search space but these may not be admissible throughout the domain thereby affecting the optimality guarantees of the search. Bounded suboptimal search using several such partially good but inadmissible heuristics was developed in Multi-Heuristic A* (MHA*). Although MHA* leverages multiple inadmissible heuristics to potentially generate a faster suboptimal solution, the original version does not improve the solution over time. It is a one shot algorithm that requires careful setting of inflation factors to obtain a desired one time solution. In this work, we tackle this issue by extending MHA* to an anytime version that finds a feasible suboptimal solution quickly and continually improves it until time runs out. Our work is inspired from the Anytime Repairing A* (ARA*) algorithm. We prove that our precise adaptation of ARA* concepts in the MHA* framework preserves the original suboptimal and completeness guarantees and enhances MHA* to perform in an anytime fashion. Furthermore, we report the performance of A-MHA* in 3-D path planning domain and sliding tiles puzzle and compare against MHA* and other anytime algorithms.

ePA*SE: Edge-based Parallel A* for Slow Evaluations

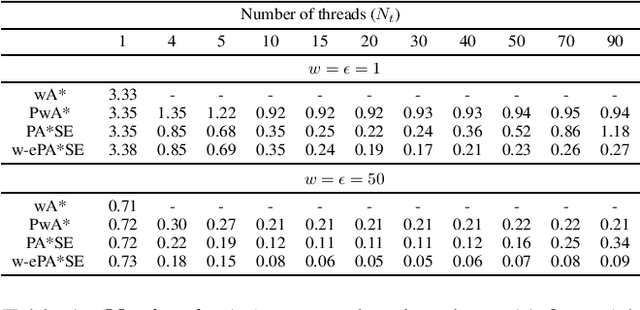
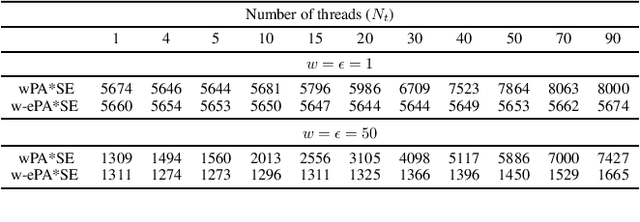
Parallel search algorithms harness the multithreading capability of modern processors to achieve faster planning. One such algorithm is PA*SE (Parallel A* for Slow Expansions), which parallelizes state expansions to achieve faster planning in domains where state expansions are slow. In this work, we propose ePA*SE (Edge-based Parallel A* for Slow Evaluations) that improves on PA*SE by parallelizing edge evaluations instead of state expansions. This makes ePA*SE more efficient in domains where edge evaluations are expensive and need varying amounts of computational effort, which is often the case in robotics. On the theoretical front, we show that ePA*SE provides rigorous optimality guarantees. In addition, ePA*SE can be trivially extended to handle an inflation weight on the heuristic resulting in a bounded suboptimal algorithm w-ePA*SE (Weighted ePA*SE) that trades off optimality for faster planning. On the experimental front, we validate the proposed algorithm in two different planning domains: 1) motion planning for 3D humanoid navigation and 2) task and motion planning for a dual-arm robotic assembly task. We show that ePA*SE can be significantly more efficient than PA*SE and other alternatives.

MPLP: Massively Parallelized Lazy Planning

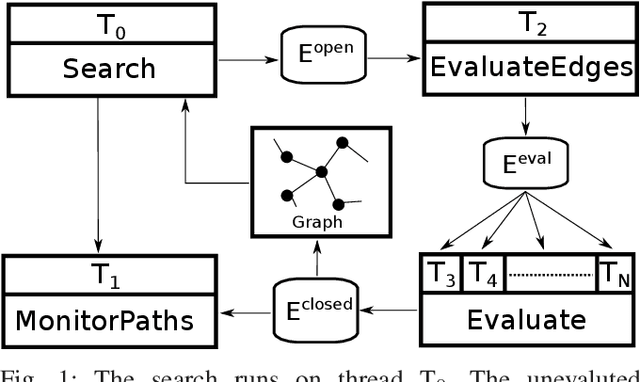
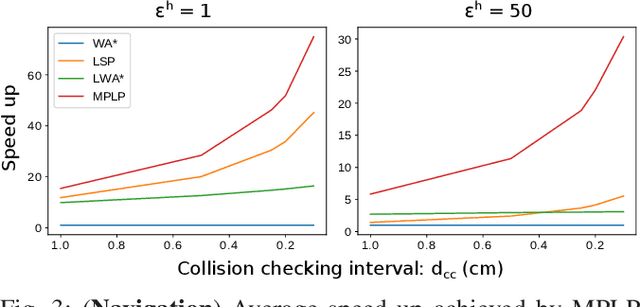
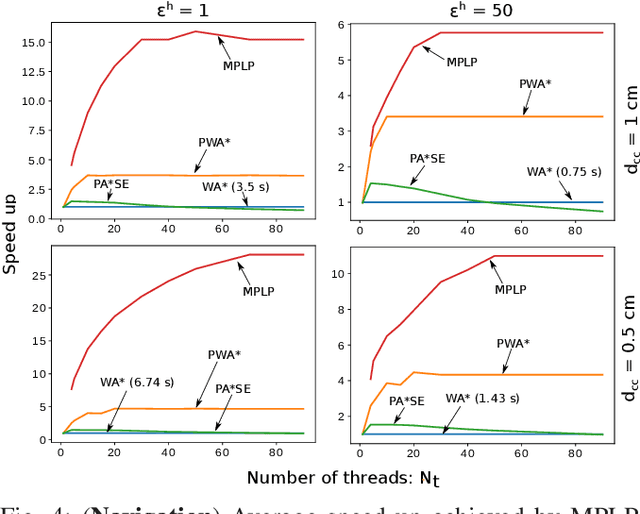
Lazy search algorithms have been developed to efficiently solve planning problems in domains where the computational effort is dominated by the cost of edge evaluation. The current approaches operate by intelligently balancing computational effort between searching the graph and evaluating edges. However these algorithms are designed to run as a single process and do not leverage the multi-threading capability of modern processors. In this work we propose a massively parallelized, bounded suboptimal, lazy search algorithm (MPLP) that harnesses modern multi-core processors. In MPLP, searching of the graph and edge evaluations are performed completely asynchronously in parallel, leading to a drastic improvement in planning time. We validate the proposed algorithm in two different planning domains: motion planning for a humanoid navigation and task and motion planning for a robotic assembly task. We show that MPLP outperforms the state of the art lazy search as well as parallel search algorithms.

Euclidean Distance-Optimal Post-Processing of Grid-Based Paths

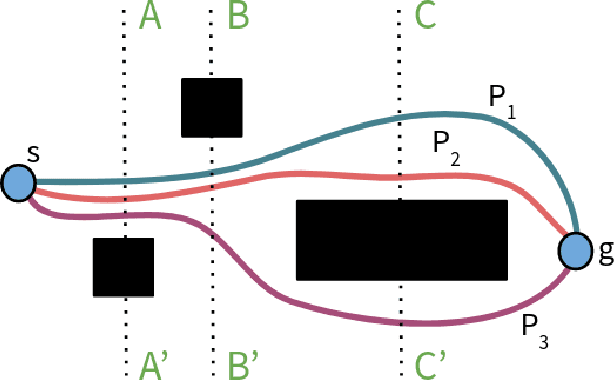
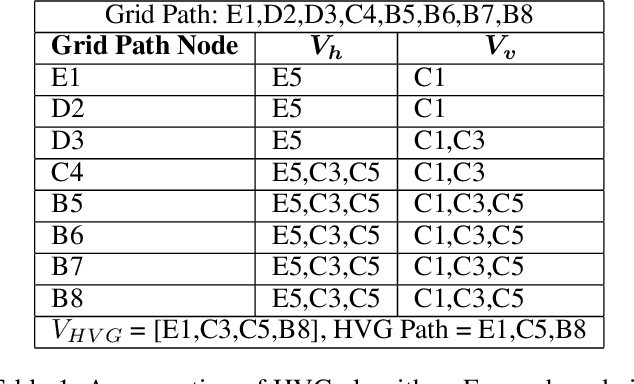
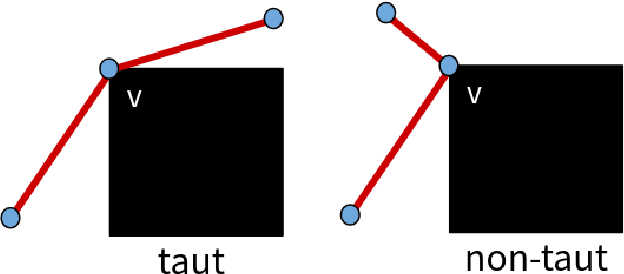
Paths planned over grids can often be suboptimal in an Euclidean space and contain a large number of unnecessary turns. Consequently, researchers have looked into post-processing techniques to improve the paths after they are planned. In this paper, we propose a novel post-processing technique, called Homotopic Visibility Graph Planning (HVG) which differentiates itself from existing post-processing methods in that it is guaranteed to shorten the path such that it is at least as short as the provably shortest path that lies within the same topological class as the initially computed path. We propose the algorithm, provide proofs and compare it experimentally against other post-processing methods and any-angle planning algorithms.