Symbolic Discovery of Stochastic Differential Equations with Genetic Programming

Automated scientific discovery aims to improve scientific understanding through machine learning. A central approach in this field is symbolic regression, which uses genetic programming or sparse regression to learn interpretable mathematical expressions to explain observed data. Conventionally, the focus of symbolic regression is on identifying ordinary differential equations. The general view is that noise only complicates the recovery of deterministic dynamics. However, explicitly learning a symbolic function of the noise component in stochastic differential equations enhances modelling capacity, increases knowledge gain and enables generative sampling. We introduce a method for symbolic discovery of stochastic differential equations based on genetic programming, jointly optimizing drift and diffusion functions via the maximum likelihood estimate. Our results demonstrate accurate recovery of governing equations, efficient scaling to higher-dimensional systems, robustness to sparsely sampled problems and generalization to stochastic partial differential equations. This work extends symbolic regression toward interpretable discovery of stochastic dynamical systems, contributing to the automation of science in a noisy and dynamic world.

Kozax: Flexible and Scalable Genetic Programming in JAX

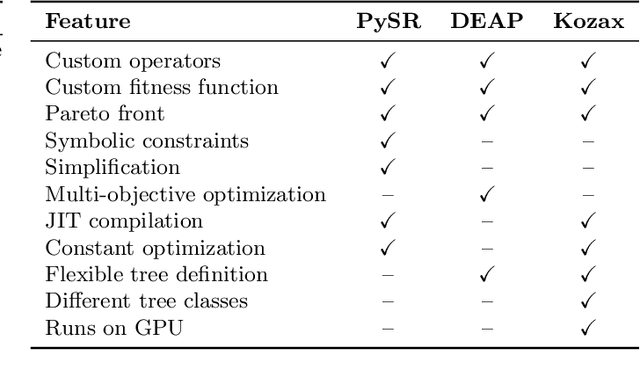
Genetic programming is an optimization algorithm inspired by natural selection which automatically evolves the structure of computer programs. The resulting computer programs are interpretable and efficient compared to black-box models with fixed structure. The fitness evaluation in genetic programming suffers from high computational requirements, limiting the performance on difficult problems. To reduce the runtime, many implementations of genetic programming require a specific data format, making the applicability limited to specific problem classes. Consequently, there is no efficient genetic programming framework that is usable for a wide range of tasks. To this end, we developed Kozax, a genetic programming framework that evolves symbolic expressions for arbitrary problems. We implemented Kozax using JAX, a framework for high-performance and scalable machine learning, which allows the fitness evaluation to scale efficiently to large populations or datasets on GPU. Furthermore, Kozax offers constant optimization, custom operator definition and simultaneous evolution of multiple trees. We demonstrate successful applications of Kozax to discover equations of natural laws, recover equations of hidden dynamic variables and evolve a control policy. Overall, Kozax provides a general, fast, and scalable library to optimize white-box solutions in the realm of scientific computing.

Closed-form control with spike coding networks

Efficient and robust control using spiking neural networks (SNNs) is still an open problem. Whilst behaviour of biological agents is produced through sparse and irregular spiking patterns, which provide both robust and efficient control, the activity patterns in most artificial spiking neural networks used for control are dense and regular -- resulting in potentially less efficient codes. Additionally, for most existing control solutions network training or optimization is necessary, even for fully identified systems, complicating their implementation in on-chip low-power solutions. The neuroscience theory of Spike Coding Networks (SCNs) offers a fully analytical solution for implementing dynamical systems in recurrent spiking neural networks -- while maintaining irregular, sparse, and robust spiking activity -- but it's not clear how to directly apply it to control problems. Here, we extend SCN theory by incorporating closed-form optimal estimation and control. The resulting networks work as a spiking equivalent of a linear-quadratic-Gaussian controller. We demonstrate robust spiking control of simulated spring-mass-damper and cart-pole systems, in the face of several perturbations, including input- and system-noise, system disturbances, and neural silencing. As our approach does not need learning or optimization, it offers opportunities for deploying fast and efficient task-specific on-chip spiking controllers with biologically realistic activity.