Variational Particle Approximations

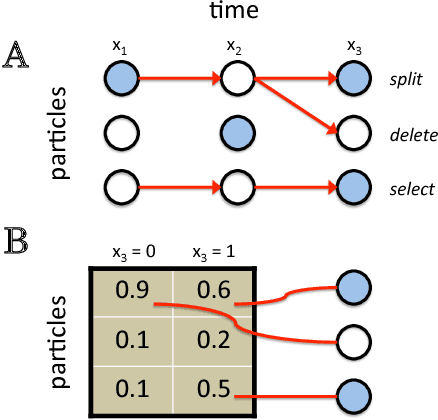
Approximate inference in high-dimensional, discrete probabilistic models is a central problem in computational statistics and machine learning. This paper describes discrete particle variational inference (DPVI), a new approach that combines key strengths of Monte Carlo, variational and search-based techniques. DPVI is based on a novel family of particle-based variational approximations that can be fit using simple, fast, deterministic search techniques. Like Monte Carlo, DPVI can handle multiple modes, and yields exact results in a well-defined limit. Like unstructured mean-field, DPVI is based on optimizing a lower bound on the partition function; when this quantity is not of intrinsic interest, it facilitates convergence assessment and debugging. Like both Monte Carlo and combinatorial search, DPVI can take advantage of factorization, sequential structure, and custom search operators. This paper defines DPVI particle-based approximation family and partition function lower bounds, along with the sequential DPVI and local DPVI algorithm templates for optimizing them. DPVI is illustrated and evaluated via experiments on lattice Markov Random Fields, nonparametric Bayesian mixtures and block-models, and parametric as well as non-parametric hidden Markov models. Results include applications to real-world spike-sorting and relational modeling problems, and show that DPVI can offer appealing time/accuracy trade-offs as compared to multiple alternatives.

Nonparametric variational inference

Variational methods are widely used for approximate posterior inference. However, their use is typically limited to families of distributions that enjoy particular conjugacy properties. To circumvent this limitation, we propose a family of variational approximations inspired by nonparametric kernel density estimation. The locations of these kernels and their bandwidth are treated as variational parameters and optimized to improve an approximate lower bound on the marginal likelihood of the data. Using multiple kernels allows the approximation to capture multiple modes of the posterior, unlike most other variational approximations. We demonstrate the efficacy of the nonparametric approximation with a hierarchical logistic regression model and a nonlinear matrix factorization model. We obtain predictive performance as good as or better than more specialized variational methods and sample-based approximations. The method is easy to apply to more general graphical models for which standard variational methods are difficult to derive.