Optimal Transport Features for Morphometric Population Analysis

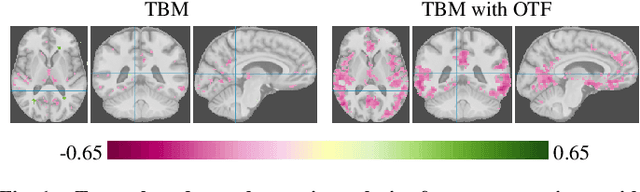
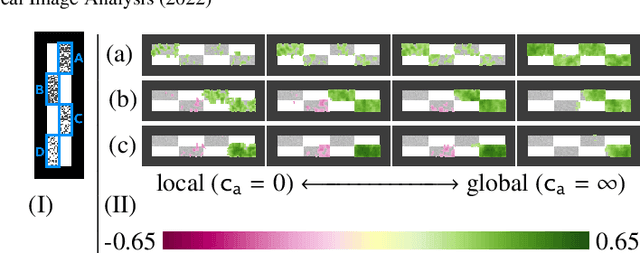
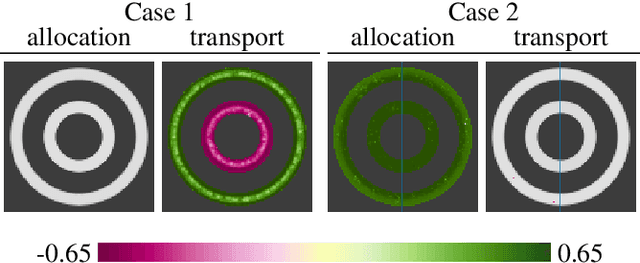
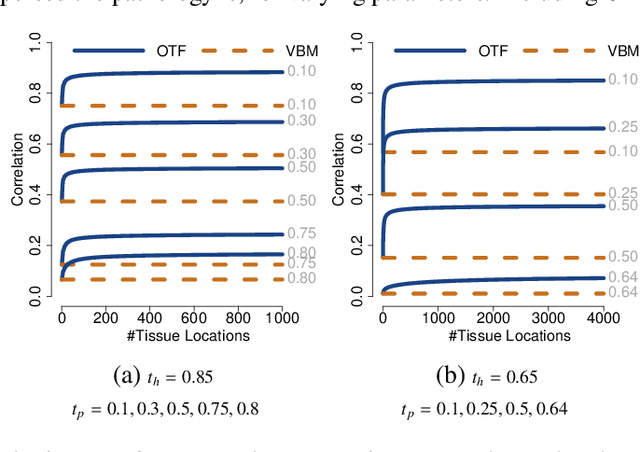
Brain pathologies often manifest as partial or complete loss of tissue. The goal of many neuroimaging studies is to capture the location and amount of tissue changes with respect to a clinical variable of interest, such as disease progression. Morphometric analysis approaches capture local differences in the distribution of tissue or other quantities of interest in relation to a clinical variable. We propose to augment morphometric analysis with an additional feature extraction step based on unbalanced optimal transport. The optimal transport feature extraction step increases statistical power for pathologies that cause spatially dispersed tissue loss, minimizes sensitivity to shifts due to spatial misalignment or differences in brain topology, and separates changes due to volume differences from changes due to tissue location. We demonstrate the proposed optimal transport feature extraction step in the context of a volumetric morphometric analysis of the OASIS-1 study for Alzheimer's disease. The results demonstrate that the proposed approach can identify tissue changes and differences that are not otherwise measurable.

Saddlepoints in Unsupervised Least Squares

This paper sheds light on the risk landscape of unsupervised least squares in the context of deep auto-encoding neural nets. We formally establish an equivalence between unsupervised least squares and principal manifolds. This link provides insight into the risk landscape of auto--encoding under the mean squared error, in particular all non-trivial critical points are saddlepoints. Finding saddlepoints is in itself difficult, overcomplete auto-encoding poses the additional challenge that the saddlepoints are degenerate. Within this context we discuss regularization of auto-encoders, in particular bottleneck, denoising and contraction auto-encoding and propose a new optimization strategy that can be framed as particular form of contractive regularization.

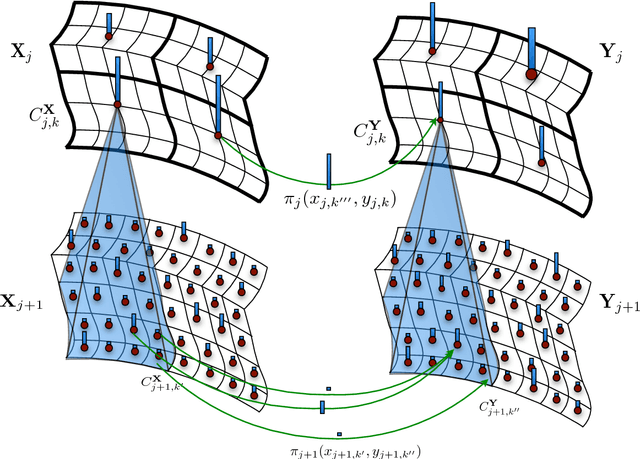
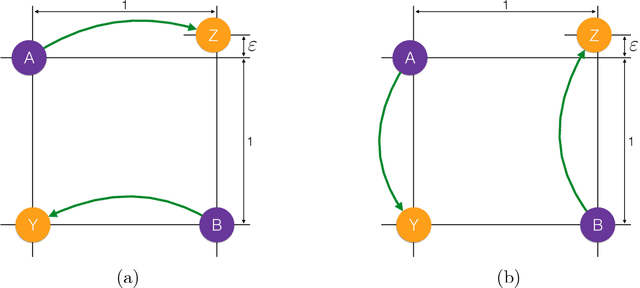
Multiscale Strategies for Computing Optimal Transport

This paper presents a multiscale approach to efficiently compute approximate optimal transport plans between point sets. It is particularly well-suited for point sets that are in high-dimensions, but are close to being intrinsically low-dimensional. The approach is based on an adaptive multiscale decomposition of the point sets. The multiscale decomposition yields a sequence of optimal transport problems, that are solved in a top-to-bottom fashion from the coarsest to the finest scale. We provide numerical evidence that this multiscale approach scales approximately linearly, in time and memory, in the number of nodes, instead of quadratically or worse for a direct solution. Empirically, the multiscale approach results in less than one percent relative error in the objective function. Furthermore, the multiscale plans constructed are of interest by themselves as they may be used to introduce novel features and notions of distances between point sets. An analysis of sets of brain MRI based on optimal transport distances illustrates the effectiveness of the proposed method on a real world data set. The application demonstrates that multiscale optimal transport distances have the potential to improve on state-of-the-art metrics currently used in computational anatomy.