Final Adaptation Reinforcement Learning for N-Player Games

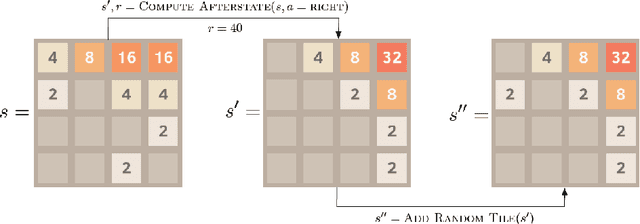
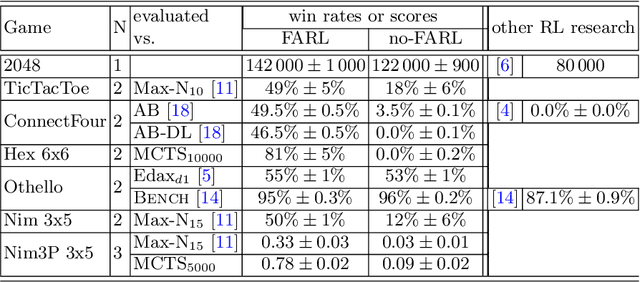
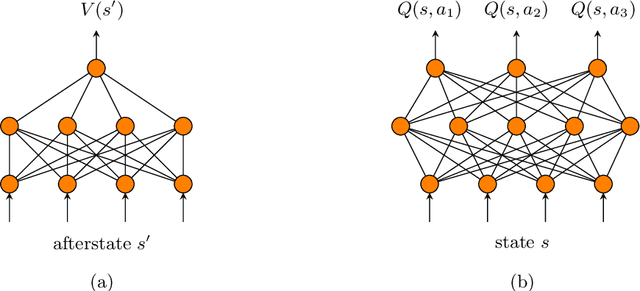
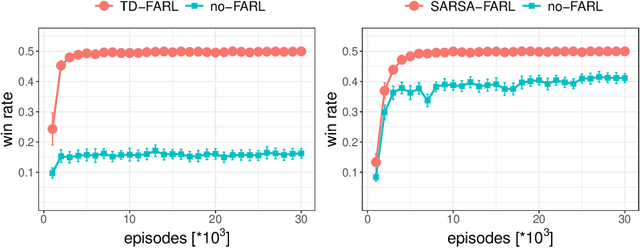
This paper covers n-tuple-based reinforcement learning (RL) algorithms for games. We present new algorithms for TD-, SARSA- and Q-learning which work seamlessly on various games with arbitrary number of players. This is achieved by taking a player-centered view where each player propagates his/her rewards back to previous rounds. We add a new element called Final Adaptation RL (FARL) to all these algorithms. Our main contribution is that FARL is a vitally important ingredient to achieve success with the player-centered view in various games. We report results on seven board games with 1, 2 and 3 players, including Othello, ConnectFour and Hex. In most cases it is found that FARL is important to learn a near-perfect playing strategy. All algorithms are available in the GBG framework on GitHub.

SACOBRA with Online Whitening for Solving Optimization Problems with High Conditioning

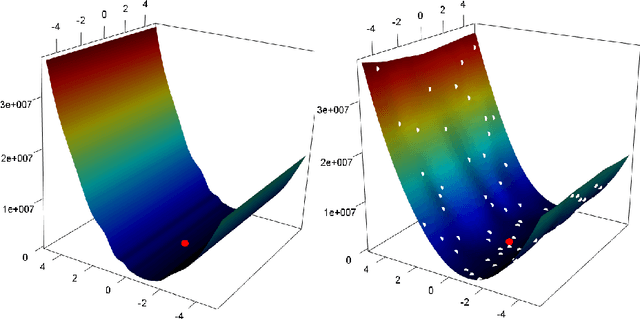
Real-world optimization problems often have expensive objective functions in terms of cost and time. It is desirable to find near-optimal solutions with very few function evaluations. Surrogate-assisted optimizers tend to reduce the required number of function evaluations by replacing the real function with an efficient mathematical model built on few evaluated points. Problems with a high condition number are a challenge for many surrogate-assisted optimizers including SACOBRA. To address such problems we propose a new online whitening operating in the black-box optimization paradigm. We show on a set of high-conditioning functions that online whitening tackles SACOBRA's early stagnation issue and reduces the optimization error by a factor between 10 to 1e12 as compared to the plain SACOBRA, though it imposes many extra function evaluations. Covariance matrix adaptation evolution strategy (CMA-ES) has for very high numbers of function evaluations even lower errors, whereas SACOBRA performs better in the expensive setting (less than 1e03 function evaluations). If we count all parallelizable function evaluations (population evaluation in CMA-ES, online whitening in our approach) as one iteration, then both algorithms have comparable strength even on the long run. This holds for problems with dimension D <= 20.

Solving the G-problems in less than 500 iterations: Improved efficient constrained optimization by surrogate modeling and adaptive parameter control

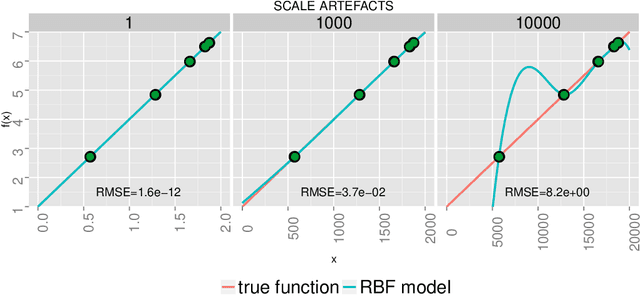
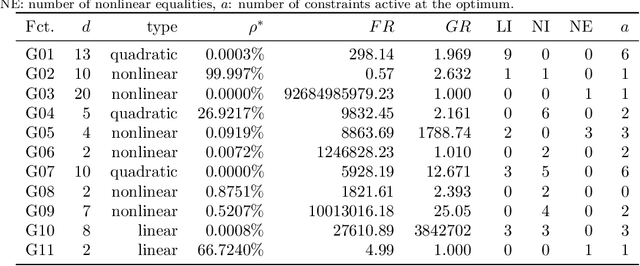
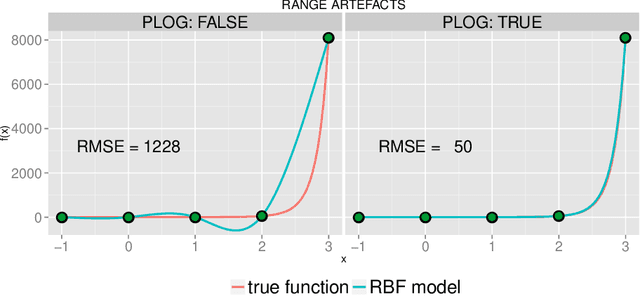
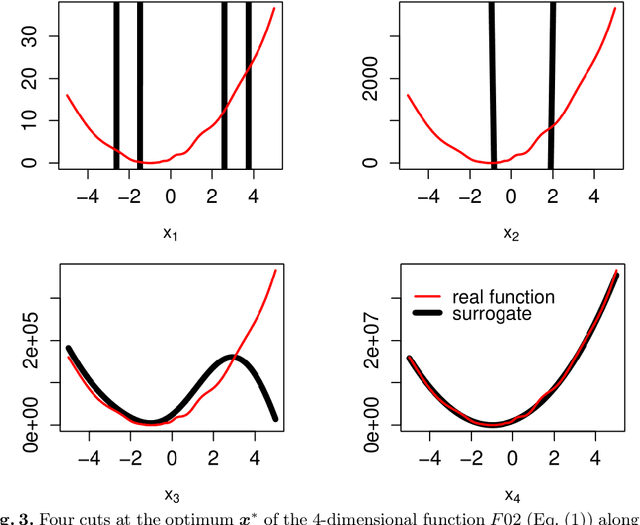
Constrained optimization of high-dimensional numerical problems plays an important role in many scientific and industrial applications. Function evaluations in many industrial applications are severely limited and no analytical information about objective function and constraint functions is available. For such expensive black-box optimization tasks, the constraint optimization algorithm COBRA was proposed, making use of RBF surrogate modeling for both the objective and the constraint functions. COBRA has shown remarkable success in solving reliably complex benchmark problems in less than 500 function evaluations. Unfortunately, COBRA requires careful adjustment of parameters in order to do so. In this work we present a new self-adjusting algorithm SACOBRA, which is based on COBRA and capable to achieve high-quality results with very few function evaluations and no parameter tuning. It is shown with the help of performance profiles on a set of benchmark problems (G-problems, MOPTA08) that SACOBRA consistently outperforms any COBRA algorithm with fixed parameter setting. We analyze the importance of the several new elements in SACOBRA and find that each element of SACOBRA plays a role to boost up the overall optimization performance. We discuss the reasons behind and get in this way a better understanding of high-quality RBF surrogate modeling.