Asymptotic Study of In-context Learning with Random Transformers through Equivalent Models

We study the in-context learning (ICL) capabilities of pretrained Transformers in the setting of nonlinear regression. Specifically, we focus on a random Transformer with a nonlinear MLP head where the first layer is randomly initialized and fixed while the second layer is trained. Furthermore, we consider an asymptotic regime where the context length, input dimension, hidden dimension, number of training tasks, and number of training samples jointly grow. In this setting, we show that the random Transformer behaves equivalent to a finite-degree Hermite polynomial model in terms of ICL error. This equivalence is validated through simulations across varying activation functions, context lengths, hidden layer widths (revealing a double-descent phenomenon), and regularization settings. Our results offer theoretical and empirical insights into when and how MLP layers enhance ICL, and how nonlinearity and over-parameterization influence model performance.

Learning Rate Should Scale Inversely with High-Order Data Moments in High-Dimensional Online Independent Component Analysis

We investigate the impact of high-order moments on the learning dynamics of an online Independent Component Analysis (ICA) algorithm under a high-dimensional data model composed of a weighted sum of two non-Gaussian random variables. This model allows precise control of the input moment structure via a weighting parameter. Building on an existing ordinary differential equation (ODE)-based analysis in the high-dimensional limit, we demonstrate that as the high-order moments increase, the algorithm exhibits slower convergence and demands both a lower learning rate and greater initial alignment to achieve informative solutions. Our findings highlight the algorithm's sensitivity to the statistical structure of the input data, particularly its moment characteristics. Furthermore, the ODE framework reveals a critical learning rate threshold necessary for learning when moments approach their maximum. These insights motivate future directions in moment-aware initialization and adaptive learning rate strategies to counteract the degradation in learning speed caused by high non-Gaussianity, thereby enhancing the robustness and efficiency of ICA in complex, high-dimensional settings.

Benefits of Online Tilted Empirical Risk Minimization: A Case Study of Outlier Detection and Robust Regression

Empirical Risk Minimization (ERM) is a foundational framework for supervised learning but primarily optimizes average-case performance, often neglecting fairness and robustness considerations. Tilted Empirical Risk Minimization (TERM) extends ERM by introducing an exponential tilt hyperparameter $t$ to balance average-case accuracy with worst-case fairness and robustness. However, in online or streaming settings where data arrive one sample at a time, the classical TERM objective degenerates to standard ERM, losing tilt sensitivity. We address this limitation by proposing an online TERM formulation that removes the logarithm from the classical objective, preserving tilt effects without additional computational or memory overhead. This formulation enables a continuous trade-off controlled by $t$, smoothly interpolating between ERM ($t \to 0$), fairness emphasis ($t > 0$), and robustness to outliers ($t < 0$). We empirically validate online TERM on two representative streaming tasks: robust linear regression with adversarial outliers and minority-class detection in binary classification. Our results demonstrate that negative tilting effectively suppresses outlier influence, while positive tilting improves recall with minimal impact on precision, all at per-sample computational cost equivalent to ERM. Online TERM thus recovers the full robustness-fairness spectrum of classical TERM in an efficient single-sample learning regime.

Random Features Outperform Linear Models: Effect of Strong Input-Label Correlation in Spiked Covariance Data

Random Feature Model (RFM) with a nonlinear activation function is instrumental in understanding training and generalization performance in high-dimensional learning. While existing research has established an asymptotic equivalence in performance between the RFM and noisy linear models under isotropic data assumptions, empirical observations indicate that the RFM frequently surpasses linear models in practical applications. To address this gap, we ask, "When and how does the RFM outperform linear models?" In practice, inputs often have additional structures that significantly influence learning. Therefore, we explore the RFM under anisotropic input data characterized by spiked covariance in the proportional asymptotic limit, where dimensions diverge jointly while maintaining finite ratios. Our analysis reveals that a high correlation between inputs and labels is a critical factor enabling the RFM to outperform linear models. Moreover, we show that the RFM performs equivalent to noisy polynomial models, where the polynomial degree depends on the strength of the correlation between inputs and labels. Our numerical simulations validate these theoretical insights, confirming the performance-wise superiority of RFM in scenarios characterized by strong input-label correlation.

Optimal Nonlinearities Improve Generalization Performance of Random Features

Random feature model with a nonlinear activation function has been shown to perform asymptotically equivalent to a Gaussian model in terms of training and generalization errors. Analysis of the equivalent model reveals an important yet not fully understood role played by the activation function. To address this issue, we study the "parameters" of the equivalent model to achieve improved generalization performance for a given supervised learning problem. We show that acquired parameters from the Gaussian model enable us to define a set of optimal nonlinearities. We provide two example classes from this set, e.g., second-order polynomial and piecewise linear functions. These functions are optimized to improve generalization performance regardless of the actual form. We experiment with regression and classification problems, including synthetic and real (e.g., CIFAR10) data. Our numerical results validate that the optimized nonlinearities achieve better generalization performance than widely-used nonlinear functions such as ReLU. Furthermore, we illustrate that the proposed nonlinearities also mitigate the so-called double descent phenomenon, which is known as the non-monotonic generalization performance regarding the sample size and the model size.

Neural Academic Paper Generation

In this work, we tackle the problem of structured text generation, specifically academic paper generation in $\LaTeX{}$, inspired by the surprisingly good results of basic character-level language models. Our motivation is using more recent and advanced methods of language modeling on a more complex dataset of $\LaTeX{}$ source files to generate realistic academic papers. Our first contribution is preparing a dataset with $\LaTeX{}$ source files on recent open-source computer vision papers. Our second contribution is experimenting with recent methods of language modeling and text generation such as Transformer and Transformer-XL to generate consistent $\LaTeX{}$ code. We report cross-entropy and bits-per-character (BPC) results of the trained models, and we also discuss interesting points on some examples of the generated $\LaTeX{}$ code.

DeepSmartFuzzer: Reward Guided Test Generation For Deep Learning

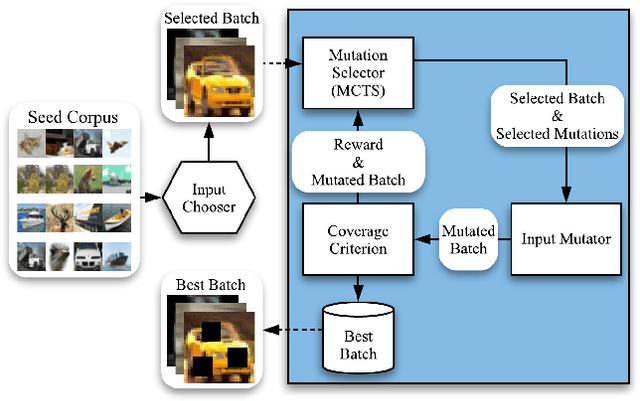
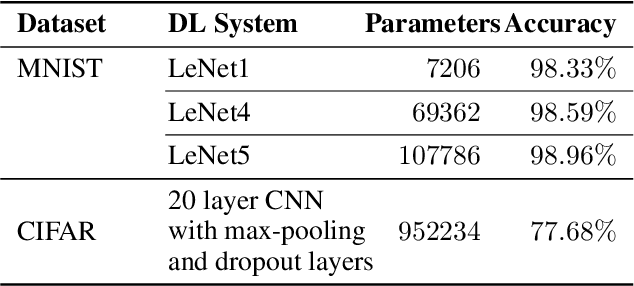
Testing Deep Neural Network (DNN) models has become more important than ever with the increasing usage of DNN models in safety-critical domains such as autonomous cars. The traditional approach of testing DNNs is to create a test set, which is a random subset of the dataset about the problem of interest. This kind of approach is not enough for testing most of the real-world scenarios since these traditional test sets do not include corner cases, while a corner case input is generally considered to introduce erroneous behaviors. Recent works on adversarial input generation, data augmentation, and coverage-guided fuzzing (CGF) have provided new ways to extend traditional test sets. Among those, CGF aims to produce new test inputs by fuzzing existing ones to achieve high coverage on a test adequacy criterion (i.e. coverage criterion). Given that the subject test adequacy criterion is a well-established one, CGF can potentially find error inducing inputs for different underlying reasons. In this paper, we propose a novel CGF solution for structural testing of DNNs. The proposed fuzzer employs Monte Carlo Tree Search to drive the coverage-guided search in the pursuit of achieving high coverage. Our evaluation shows that the inputs generated by our method result in higher coverage than the inputs produced by the previously introduced coverage-guided fuzzing techniques.