Saeid Sedighi
MIMO Radar Transmit Beampattern Shaping for Spectrally Dense Environments
Dec 13, 2021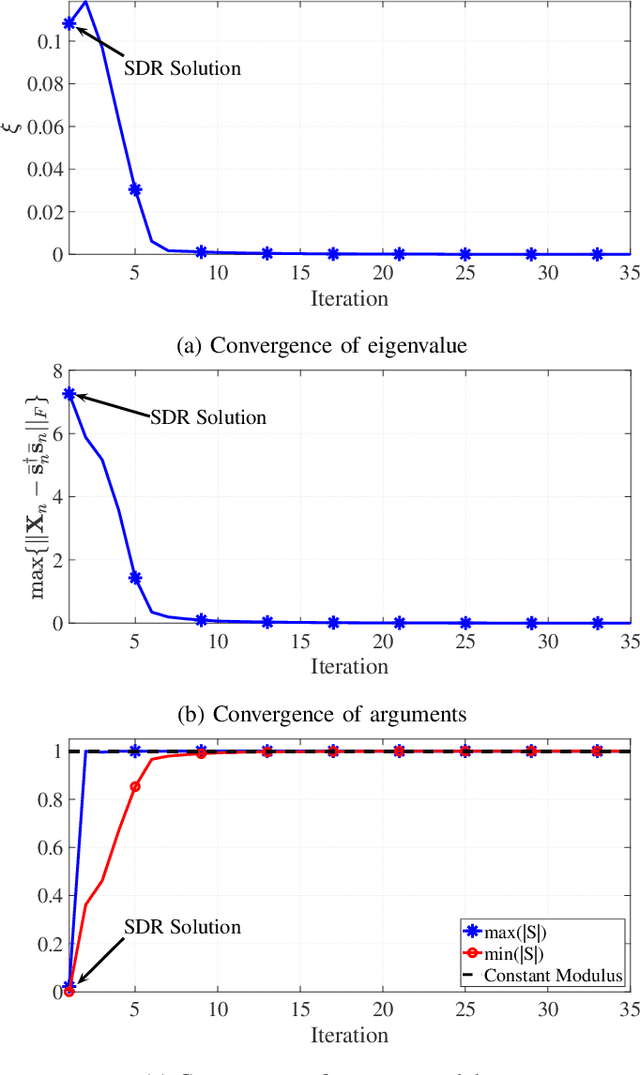

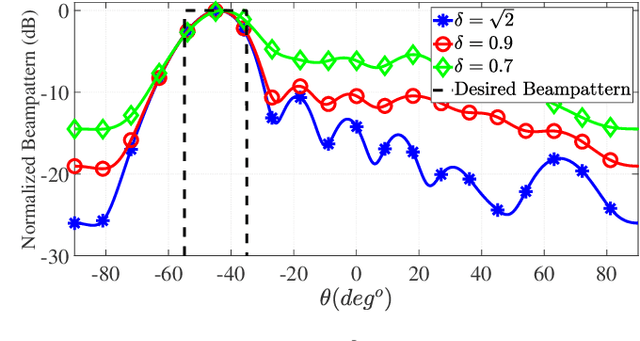

Abstract:Designing unimodular waveforms with a desired beampattern, spectral occupancy and orthogonality level is of vital importance in the next generation Multiple-Input Multiple-Output (MIMO) radar systems. Motivated by this fact, in this paper, we propose a framework for shaping the beampattern in MIMO radar systems under the constraints simultaneously ensuring unimodularity, desired spectral occupancy and orthogonality of the designed waveform. In this manner, the proposed framework is the most comprehensive approach for MIMO radar waveform design focusing on beampattern shaping. The problem formulation leads to a non-convex quadratic fractional programming. We propose an effective iterative to solve the problem, where each iteration is composed of a Semi-Definite Programming (SDP) followed by eigenvalue decomposition. Some numerical simulations are provided to illustrate the superior performance of our proposed over the state-of-the-art.
On the Performance of One-Bit DoA Estimation via Sparse Linear Arrays
Dec 28, 2020

Abstract:Direction of Arrival (DoA) estimation using Sparse Linear Arrays (SLAs) has recently gained considerable attention in array processing thanks to their capability to provide enhanced degrees of freedom in resolving uncorrelated source signals. Additionally, deployment of one-bit Analog-to-Digital Converters (ADCs) has emerged as an important topic in array processing, as it offers both a low-cost and a low-complexity implementation. In this paper, we study the problem of DoA estimation from one-bit measurements received by an SLA. Specifically, we first investigate the identifiability conditions for the DoA estimation problem from one-bit SLA data and establish an equivalency with the case when DoAs are estimated from infinite-bit unquantized measurements. Towards determining the performance limits of DoA estimation from one-bit quantized data, we derive a pessimistic approximation of the corresponding Cram\'{e}r-Rao Bound (CRB). This pessimistic CRB is then used as a benchmark for assessing the performance of one-bit DoA estimators. We also propose a new algorithm for estimating DoAs from one-bit quantized data. We investigate the analytical performance of the proposed method through deriving a closed-form expression for the covariance matrix of the asymptotic distribution of the DoA estimation errors and show that it outperforms the existing algorithms in the literature. Numerical simulations are provided to validate the analytical derivations and corroborate the resulting performance improvement.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge