Graph Unfolding and Sampling for Transitory Video Summarization via Gershgorin Disc Alignment

User-generated videos (UGVs) uploaded from mobile phones to social media sites like YouTube and TikTok are short and non-repetitive. We summarize a transitory UGV into several keyframes in linear time via fast graph sampling based on Gershgorin disc alignment (GDA). Specifically, we first model a sequence of $N$ frames in a UGV as an $M$-hop path graph $\mathcal{G}^o$ for $M \ll N$, where the similarity between two frames within $M$ time instants is encoded as a positive edge based on feature similarity. Towards efficient sampling, we then "unfold" $\mathcal{G}^o$ to a $1$-hop path graph $\mathcal{G}$, specified by a generalized graph Laplacian matrix $\mathcal{L}$, via one of two graph unfolding procedures with provable performance bounds. We show that maximizing the smallest eigenvalue $\lambda_{\min}(\mathbf{B})$ of a coefficient matrix $\mathbf{B} = \textit{diag}\left(\mathbf{h}\right) + \mu \mathcal{L}$, where $\mathbf{h}$ is the binary keyframe selection vector, is equivalent to minimizing a worst-case signal reconstruction error. We maximize instead the Gershgorin circle theorem (GCT) lower bound $\lambda^-_{\min}(\mathbf{B})$ by choosing $\mathbf{h}$ via a new fast graph sampling algorithm that iteratively aligns left-ends of Gershgorin discs for all graph nodes (frames). Extensive experiments on multiple short video datasets show that our algorithm achieves comparable or better video summarization performance compared to state-of-the-art methods, at a substantially reduced complexity.

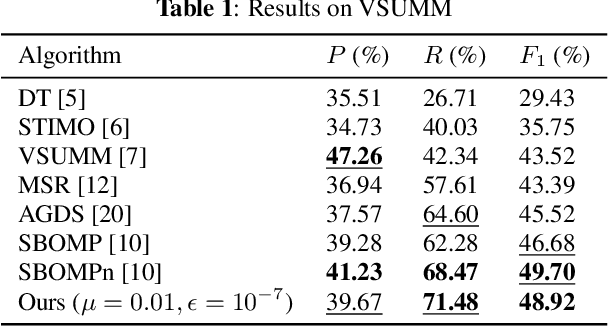
Fast Graph Sampling for Short Video Summarization using Gershgorin Disc Alignment

We study the problem of efficiently summarizing a short video into several keyframes, leveraging recent progress in fast graph sampling. Specifically, we first construct a similarity path graph (SPG) $\mathcal{G}$, represented by graph Laplacian matrix $\mathbf{L}$, where the similarities between adjacent frames are encoded as positive edge weights. We show that maximizing the smallest eigenvalue $\lambda_{\min}(\mathbf{B})$ of a coefficient matrix $\mathbf{B} = \text{diag}(\mathbf{a}) + \mu \mathbf{L}$, where $\mathbf{a}$ is the binary keyframe selection vector, is equivalent to minimizing a worst-case signal reconstruction error. We prove that, after partitioning $\mathcal{G}$ into $Q$ sub-graphs $\{\mathcal{G}^q\}^Q_{q=1}$, the smallest Gershgorin circle theorem (GCT) lower bound of $Q$ corresponding coefficient matrices -- $\min_q \lambda^-_{\min}(\mathbf{B}^q)$ -- is a lower bound for $\lambda_{\min}(\mathbf{B})$. This inspires a fast graph sampling algorithm to iteratively partition $\mathcal{G}$ into $Q$ sub-graphs using $Q$ samples (keyframes), while maximizing $\lambda^-_{\min}(\mathbf{B}^q)$ for each sub-graph $\mathcal{G}^q$. Experimental results show that our algorithm achieves comparable video summarization performance as state-of-the-art methods, at a substantially reduced complexity.