Fast Graph Sampling for Short Video Summarization using Gershgorin Disc Alignment
Paper and Code
Oct 25, 2021
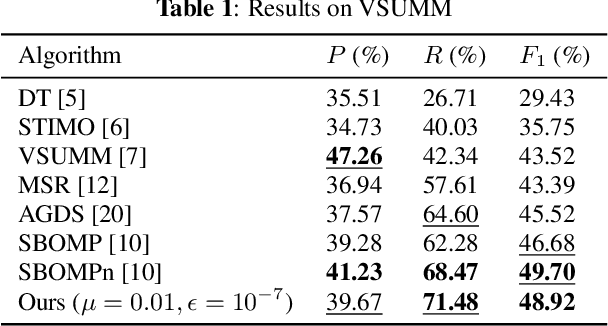

We study the problem of efficiently summarizing a short video into several keyframes, leveraging recent progress in fast graph sampling. Specifically, we first construct a similarity path graph (SPG) $\mathcal{G}$, represented by graph Laplacian matrix $\mathbf{L}$, where the similarities between adjacent frames are encoded as positive edge weights. We show that maximizing the smallest eigenvalue $\lambda_{\min}(\mathbf{B})$ of a coefficient matrix $\mathbf{B} = \text{diag}(\mathbf{a}) + \mu \mathbf{L}$, where $\mathbf{a}$ is the binary keyframe selection vector, is equivalent to minimizing a worst-case signal reconstruction error. We prove that, after partitioning $\mathcal{G}$ into $Q$ sub-graphs $\{\mathcal{G}^q\}^Q_{q=1}$, the smallest Gershgorin circle theorem (GCT) lower bound of $Q$ corresponding coefficient matrices -- $\min_q \lambda^-_{\min}(\mathbf{B}^q)$ -- is a lower bound for $\lambda_{\min}(\mathbf{B})$. This inspires a fast graph sampling algorithm to iteratively partition $\mathcal{G}$ into $Q$ sub-graphs using $Q$ samples (keyframes), while maximizing $\lambda^-_{\min}(\mathbf{B}^q)$ for each sub-graph $\mathcal{G}^q$. Experimental results show that our algorithm achieves comparable video summarization performance as state-of-the-art methods, at a substantially reduced complexity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge