Conditional Coverage Diagnostics for Conformal Prediction

Evaluating conditional coverage remains one of the most persistent challenges in assessing the reliability of predictive systems. Although conformal methods can give guarantees on marginal coverage, no method can guarantee to produce sets with correct conditional coverage, leaving practitioners without a clear way to interpret local deviations. To overcome sample-inefficiency and overfitting issues of existing metrics, we cast conditional coverage estimation as a classification problem. Conditional coverage is violated if and only if any classifier can achieve lower risk than the target coverage. Through the choice of a (proper) loss function, the resulting risk difference gives a conservative estimate of natural miscoverage measures such as L1 and L2 distance, and can even separate the effects of over- and under-coverage, and non-constant target coverages. We call the resulting family of metrics excess risk of the target coverage (ERT). We show experimentally that the use of modern classifiers provides much higher statistical power than simple classifiers underlying established metrics like CovGap. Additionally, we use our metric to benchmark different conformal prediction methods. Finally, we release an open-source package for ERT as well as previous conditional coverage metrics. Together, these contributions provide a new lens for understanding, diagnosing, and improving the conditional reliability of predictive systems.

Multivariate Conformal Prediction via Conformalized Gaussian Scoring

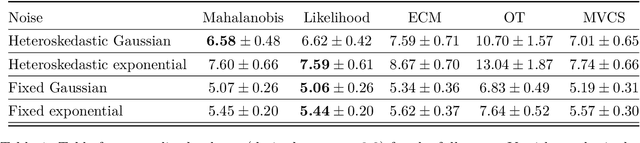
While achieving exact conditional coverage in conformal prediction is unattainable without making strong, untestable regularity assumptions, the promise of conformal prediction hinges on finding approximations to conditional guarantees that are realizable in practice. A promising direction for obtaining conditional dependence for conformal sets--in particular capturing heteroskedasticity--is through estimating the conditional density $\mathbb{P}_{Y|X}$ and conformalizing its level sets. Previous work in this vein has focused on nonconformity scores based on the empirical cumulative distribution function (CDF). Such scores are, however, computationally costly, typically requiring expensive sampling methods. To avoid the need for sampling, we observe that the CDF-based score reduces to a Mahalanobis distance in the case of Gaussian scores, yielding a closed-form expression that can be directly conformalized. Moreover, the use of a Gaussian-based score opens the door to a number of extensions of the basic conformal method; in particular, we show how to construct conformal sets with missing output values, refine conformal sets as partial information about $Y$ becomes available, and construct conformal sets on transformations of the output space. Finally, empirical results indicate that our approach produces conformal sets that more closely approximate conditional coverage in multivariate settings compared to alternative methods.

Minimum Volume Conformal Sets for Multivariate Regression

Conformal prediction provides a principled framework for constructing predictive sets with finite-sample validity. While much of the focus has been on univariate response variables, existing multivariate methods either impose rigid geometric assumptions or rely on flexible but computationally expensive approaches that do not explicitly optimize prediction set volume. We propose an optimization-driven framework based on a novel loss function that directly learns minimum-volume covering sets while ensuring valid coverage. This formulation naturally induces a new nonconformity score for conformal prediction, which adapts to the residual distribution and covariates. Our approach optimizes over prediction sets defined by arbitrary norm balls, including single and multi-norm formulations. Additionally, by jointly optimizing both the predictive model and predictive uncertainty, we obtain prediction sets that are tight, informative, and computationally efficient, as demonstrated in our experiments on real-world datasets.