RECS: Robust Graph Embedding Using Connection Subgraphs

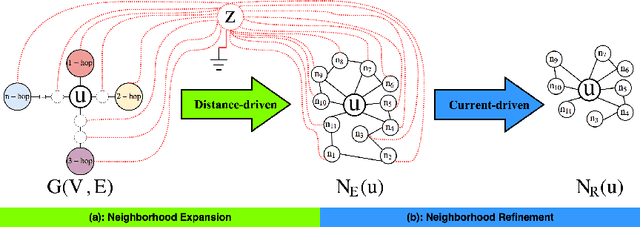
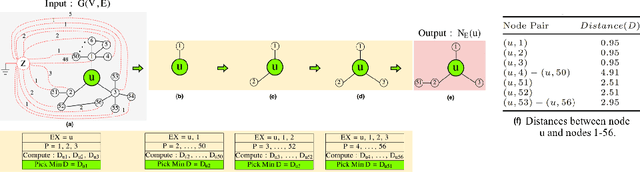
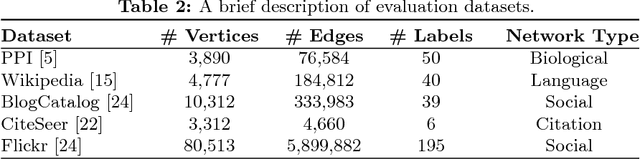
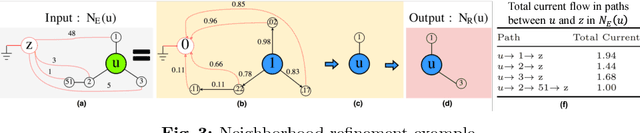
The success of graph embeddings or node representation learning in a variety of downstream tasks, such as node classification, link prediction, and recommendation systems, has led to their popularity in recent years. Representation learning algorithms aim to preserve local and global network structure by identifying node neighborhood notions. However, many existing algorithms generate embeddings that fail to properly preserve the network structure, or lead to unstable representations due to random processes (e.g., random walks to generate context) and, thus, cannot generate to multi-graph problems. In this paper, we propose RECS, a novel, stable graph embedding algorithmic framework. RECS learns graph representations using connection subgraphs by employing the analogy of graphs with electrical circuits. It preserves both local and global connectivity patterns, and addresses the issue of high-degree nodes. Further, it exploits the strength of weak ties and meta-data that have been neglected by baselines. The experiments show that RECS outperforms state-of-the-art algorithms by up to 36.85% on multi-label classification problem. Further, in contrast to baselines, RECS, being deterministic, is completely stable.

t-PINE: Tensor-based Predictable and Interpretable Node Embeddings

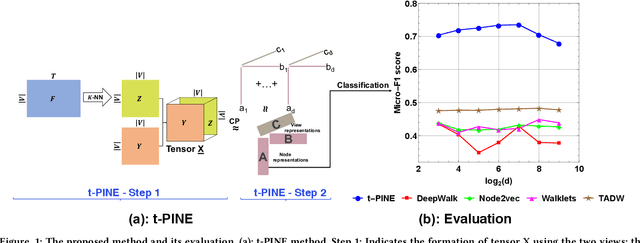
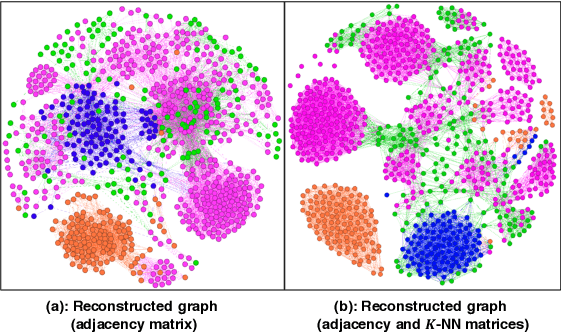
Graph representations have increasingly grown in popularity during the last years. Existing representation learning approaches explicitly encode network structure. Despite their good performance in downstream processes (e.g., node classification, link prediction), there is still room for improvement in different aspects, like efficacy, visualization, and interpretability. In this paper, we propose, t-PINE, a method that addresses these limitations. Contrary to baseline methods, which generally learn explicit graph representations by solely using an adjacency matrix, t-PINE avails a multi-view information graph, the adjacency matrix represents the first view, and a nearest neighbor adjacency, computed over the node features, is the second view, in order to learn explicit and implicit node representations, using the Canonical Polyadic (a.k.a. CP) decomposition. We argue that the implicit and the explicit mapping from a higher-dimensional to a lower-dimensional vector space is the key to learn more useful, highly predictable, and gracefully interpretable representations. Having good interpretable representations provides a good guidance to understand how each view contributes to the representation learning process. In addition, it helps us to exclude unrelated dimensions. Extensive experiments show that t-PINE drastically outperforms baseline methods by up to 158.6% with respect to Micro-F1, in several multi-label classification problems, while it has high visualization and interpretability utility.