Scaling up Stochastic Gradient Descent for Non-convex Optimisation

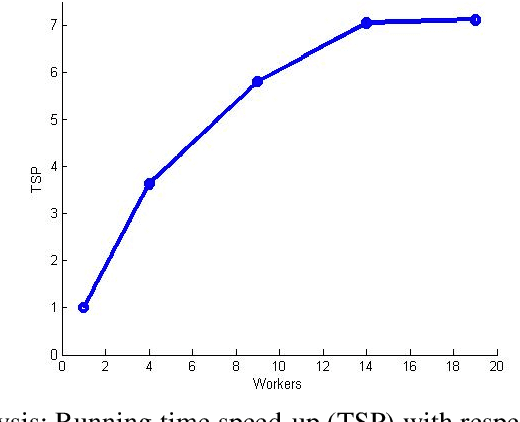
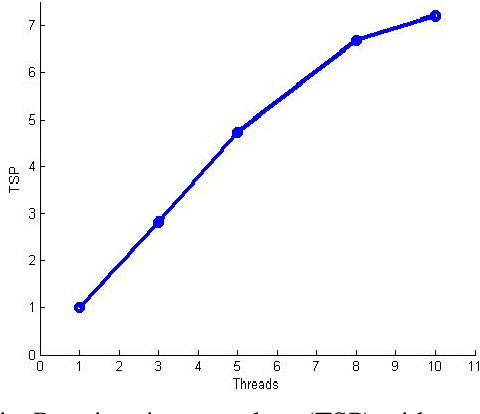
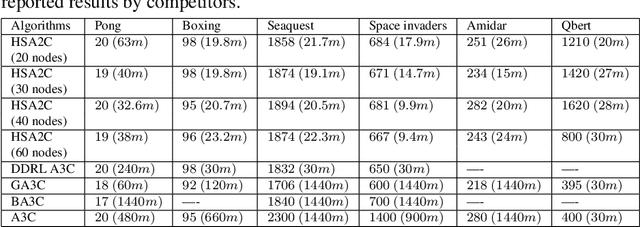
Stochastic gradient descent (SGD) is a widely adopted iterative method for optimizing differentiable objective functions. In this paper, we propose and discuss a novel approach to scale up SGD in applications involving non-convex functions and large datasets. We address the bottleneck problem arising when using both shared and distributed memory. Typically, the former is bounded by limited computation resources and bandwidth whereas the latter suffers from communication overheads. We propose a unified distributed and parallel implementation of SGD (named DPSGD) that relies on both asynchronous distribution and lock-free parallelism. By combining two strategies into a unified framework, DPSGD is able to strike a better trade-off between local computation and communication. The convergence properties of DPSGD are studied for non-convex problems such as those arising in statistical modelling and machine learning. Our theoretical analysis shows that DPSGD leads to speed-up with respect to the number of cores and number of workers while guaranteeing an asymptotic convergence rate of $O(1/\sqrt{T})$ given that the number of cores is bounded by $T^{1/4}$ and the number of workers is bounded by $T^{1/2}$ where $T$ is the number of iterations. The potential gains that can be achieved by DPSGD are demonstrated empirically on a stochastic variational inference problem (Latent Dirichlet Allocation) and on a deep reinforcement learning (DRL) problem (advantage actor critic - A2C) resulting in two algorithms: DPSVI and HSA2C. Empirical results validate our theoretical findings. Comparative studies are conducted to show the performance of the proposed DPSGD against the state-of-the-art DRL algorithms.

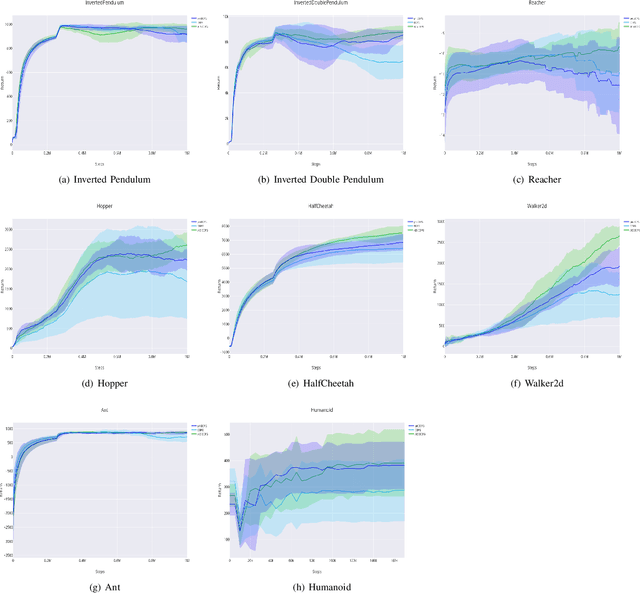
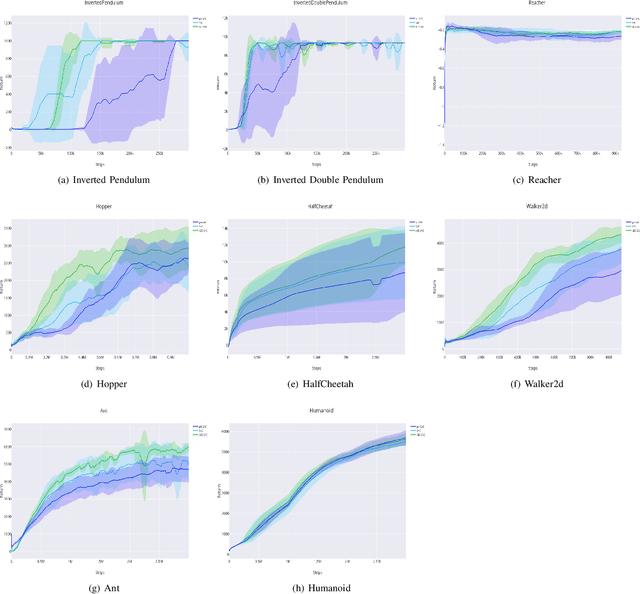
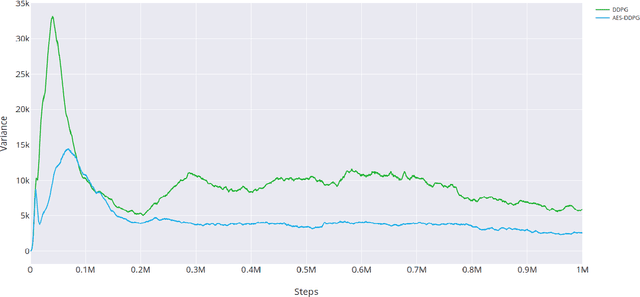
Adaptive Experience Selection for Policy Gradient

Policy gradient reinforcement learning (RL) algorithms have achieved impressive performance in challenging learning tasks such as continuous control, but suffer from high sample complexity. Experience replay is a commonly used approach to improve sample efficiency, but gradient estimators using past trajectories typically have high variance. Existing sampling strategies for experience replay like uniform sampling or prioritised experience replay do not explicitly try to control the variance of the gradient estimates. In this paper, we propose an online learning algorithm, adaptive experience selection (AES), to adaptively learn an experience sampling distribution that explicitly minimises this variance. Using a regret minimisation approach, AES iteratively updates the experience sampling distribution to match the performance of a competitor distribution assumed to have optimal variance. Sample non-stationarity is addressed by proposing a dynamic (i.e. time changing) competitor distribution for which a closed-form solution is proposed. We demonstrate that AES is a low-regret algorithm with reasonable sample complexity. Empirically, AES has been implemented for deep deterministic policy gradient and soft actor critic algorithms, and tested on 8 continuous control tasks from the OpenAI Gym library. Ours results show that AES leads to significantly improved performance compared to currently available experience sampling strategies for policy gradient.

Online Gaussian LDA for Unsupervised Pattern Mining from Utility Usage Data

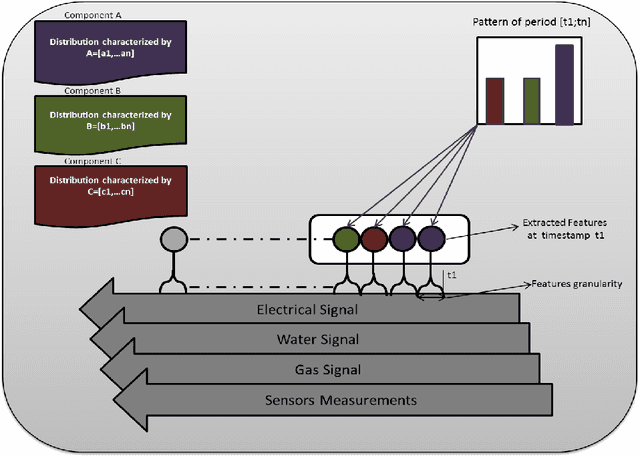
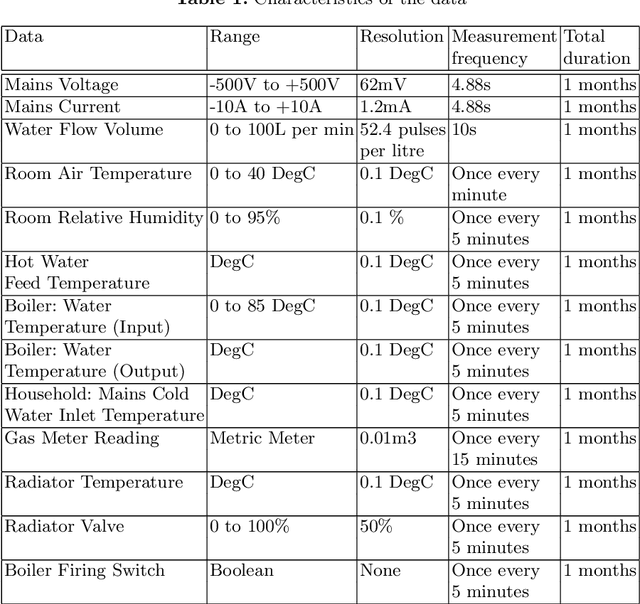
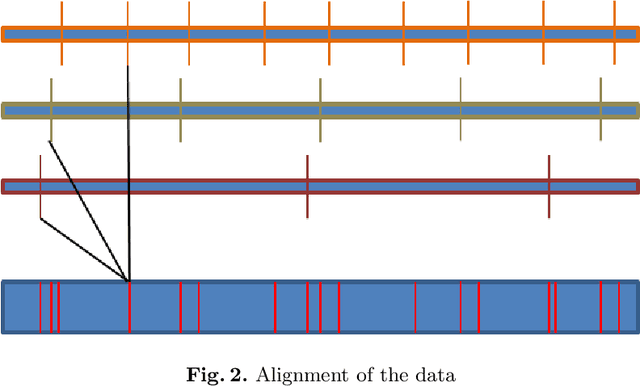
Non-intrusive load monitoring (NILM) aims at separating a whole-home energy signal into its appliance components. Such method can be harnessed to provide various services to better manage and control energy consumption (optimal planning and saving). NILM has been traditionally approached from signal processing and electrical engineering perspectives. Recently, machine learning has started to play an important role in NILM. While most work has focused on supervised algorithms, unsupervised approaches can be more interesting and of practical use in real case scenarios. Specifically, they do not require labelled training data to be acquired from individual appliances and the algorithm can be deployed to operate on the measured aggregate data directly. In this paper, we propose a fully unsupervised NILM framework based on Bayesian hierarchical mixture models. In particular, we develop a new method based on Gaussian Latent Dirichlet Allocation (GLDA) in order to extract global components that summarise the energy signal. These components provide a representation of the consumption patterns. Designed to cope with big data, our algorithm, unlike existing NILM ones, does not focus on appliance recognition. To handle this massive data, GLDA works online. Another novelty of this work compared to the existing NILM is that the data involves different utilities (e.g, electricity, water and gas) as well as some sensors measurements. Finally, we propose different evaluation methods to analyse the results which show that our algorithm finds useful patterns.

Asynchronous Stochastic Variational Inference

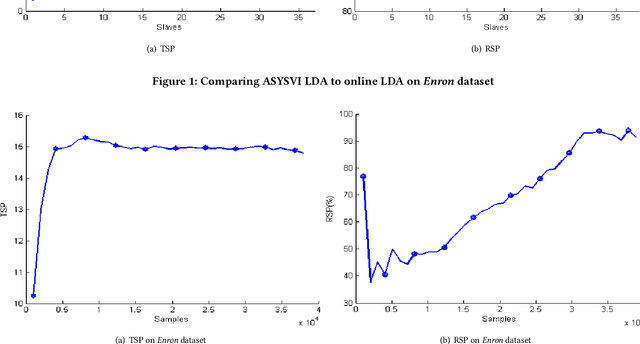
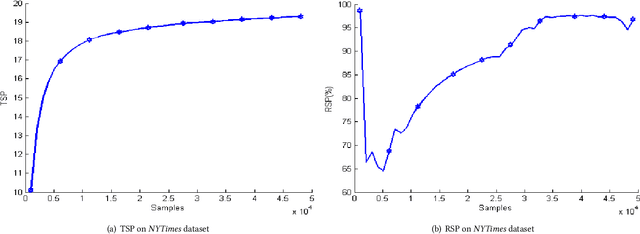
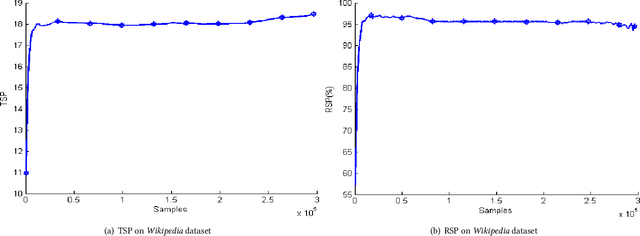
Stochastic variational inference (SVI) employs stochastic optimization to scale up Bayesian computation to massive data. Since SVI is at its core a stochastic gradient-based algorithm, horizontal parallelism can be harnessed to allow larger scale inference. We propose a lock-free parallel implementation for SVI which allows distributed computations over multiple slaves in an asynchronous style. We show that our implementation leads to linear speed-up while guaranteeing an asymptotic ergodic convergence rate $O(1/\sqrt(T)$ ) given that the number of slaves is bounded by $\sqrt(T)$ ($T$ is the total number of iterations). The implementation is done in a high-performance computing (HPC) environment using message passing interface (MPI) for python (MPI4py). The extensive empirical evaluation shows that our parallel SVI is lossless, performing comparably well to its counterpart serial SVI with linear speed-up.