Ryo Ishiyama
Symbol-Aware Reasoning with Masked Discrete Diffusion for Handwritten Mathematical Expression Recognition
Feb 03, 2026Abstract:Handwritten Mathematical Expression Recognition (HMER) requires reasoning over diverse symbols and 2D structural layouts, yet autoregressive models struggle with exposure bias and syntactic inconsistency. We present a discrete diffusion framework that reformulates HMER as iterative symbolic refinement instead of sequential generation. Through multi-step remasking, the proposal progressively refines both symbols and structural relations, removing causal dependencies and improving structural consistency. A symbol-aware tokenization and Random-Masking Mutual Learning further enhance syntactic alignment and robustness to handwriting diversity. On the MathWriting benchmark, the proposal achieves 5.56\% CER and 60.42\% EM, outperforming strong Transformer and commercial baselines. Consistent gains on CROHME 2014--2023 demonstrate that discrete diffusion provides a new paradigm for structure-aware visual recognition beyond generative modeling.
Test-Time Augmentation for Traveling Salesperson Problem
May 08, 2024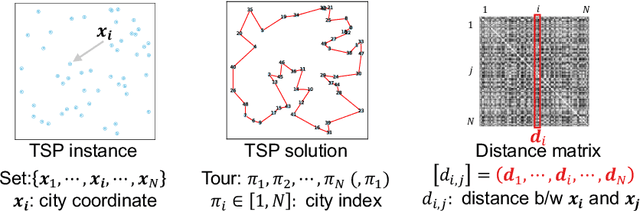
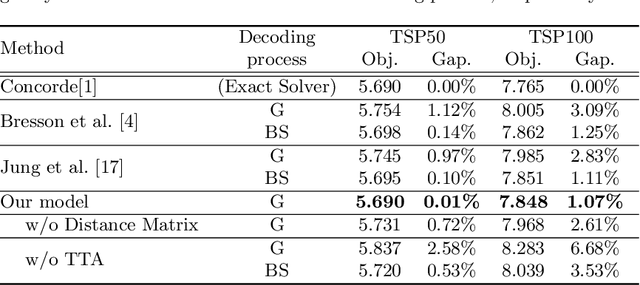
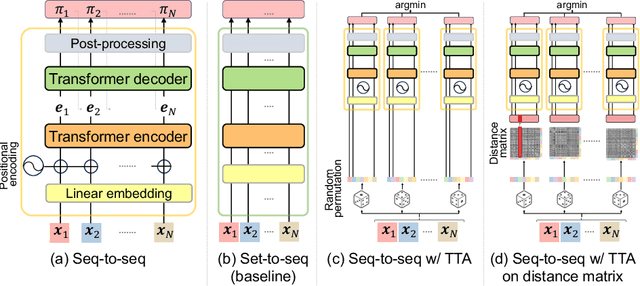
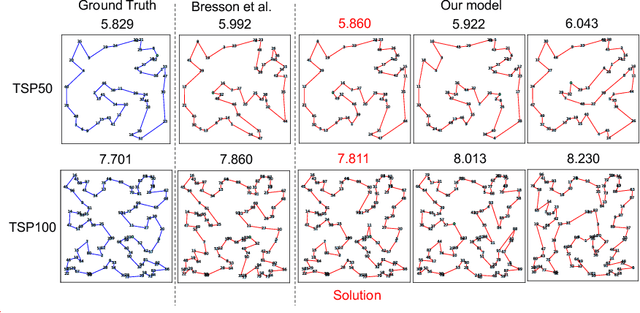
Abstract:We propose Test-Time Augmentation (TTA) as an effective technique for addressing combinatorial optimization problems, including the Traveling Salesperson Problem. In general, deep learning models possessing the property of invariance, where the output is uniquely determined regardless of the node indices, have been proposed to learn graph structures efficiently. In contrast, we interpret the permutation of node indices, which exchanges the elements of the distance matrix, as a TTA scheme. The results demonstrate that our method is capable of obtaining shorter solutions than the latest models. Furthermore, we show that the probability of finding a solution closer to an exact solution increases depending on the augmentation size.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge