Multi-Modal Molecular Representation Learning via Structure Awareness

Accurate extraction of molecular representations is a critical step in the drug discovery process. In recent years, significant progress has been made in molecular representation learning methods, among which multi-modal molecular representation methods based on images, and 2D/3D topologies have become increasingly mainstream. However, existing these multi-modal approaches often directly fuse information from different modalities, overlooking the potential of intermodal interactions and failing to adequately capture the complex higher-order relationships and invariant features between molecules. To overcome these challenges, we propose a structure-awareness-based multi-modal self-supervised molecular representation pre-training framework (MMSA) designed to enhance molecular graph representations by leveraging invariant knowledge between molecules. The framework consists of two main modules: the multi-modal molecular representation learning module and the structure-awareness module. The multi-modal molecular representation learning module collaboratively processes information from different modalities of the same molecule to overcome intermodal differences and generate a unified molecular embedding. Subsequently, the structure-awareness module enhances the molecular representation by constructing a hypergraph structure to model higher-order correlations between molecules. This module also introduces a memory mechanism for storing typical molecular representations, aligning them with memory anchors in the memory bank to integrate invariant knowledge, thereby improving the model generalization ability. Extensive experiments have demonstrated the effectiveness of MMSA, which achieves state-of-the-art performance on the MoleculeNet benchmark, with average ROC-AUC improvements ranging from 1.8% to 9.6% over baseline methods.

AS-GCL: Asymmetric Spectral Augmentation on Graph Contrastive Learning

Graph Contrastive Learning (GCL) has emerged as the foremost approach for self-supervised learning on graph-structured data. GCL reduces reliance on labeled data by learning robust representations from various augmented views. However, existing GCL methods typically depend on consistent stochastic augmentations, which overlook their impact on the intrinsic structure of the spectral domain, thereby limiting the model's ability to generalize effectively. To address these limitations, we propose a novel paradigm called AS-GCL that incorporates asymmetric spectral augmentation for graph contrastive learning. A typical GCL framework consists of three key components: graph data augmentation, view encoding, and contrastive loss. Our method introduces significant enhancements to each of these components. Specifically, for data augmentation, we apply spectral-based augmentation to minimize spectral variations, strengthen structural invariance, and reduce noise. With respect to encoding, we employ parameter-sharing encoders with distinct diffusion operators to generate diverse, noise-resistant graph views. For contrastive loss, we introduce an upper-bound loss function that promotes generalization by maintaining a balanced distribution of intra- and inter-class distance. To our knowledge, we are the first to encode augmentation views of the spectral domain using asymmetric encoders. Extensive experiments on eight benchmark datasets across various node-level tasks demonstrate the advantages of the proposed method.

Communication-Efficient Personalized Federal Graph Learning via Low-Rank Decomposition

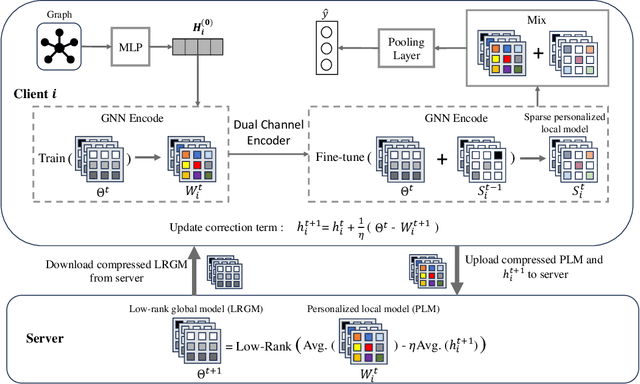
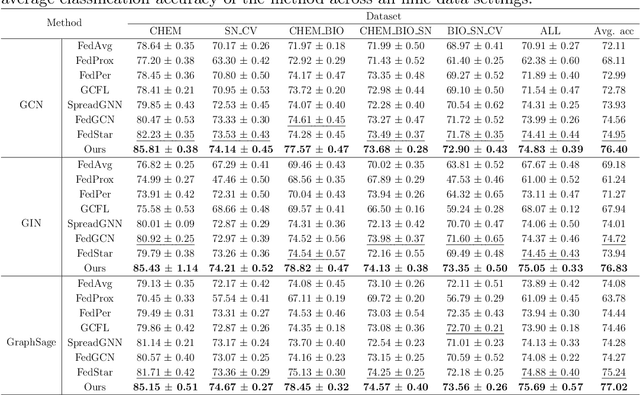
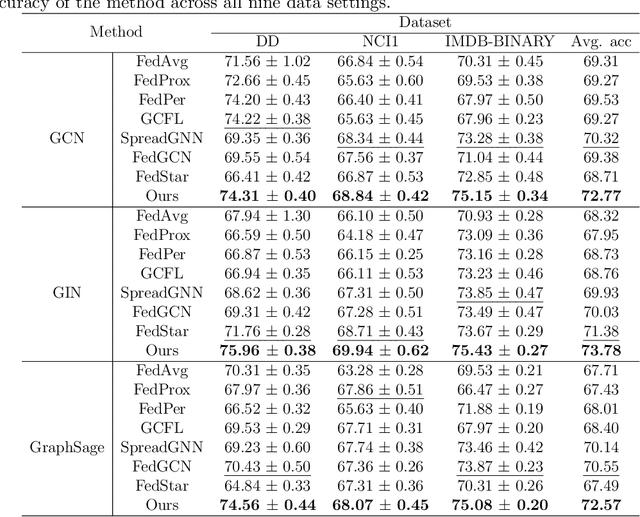
Federated graph learning (FGL) has gained significant attention for enabling heterogeneous clients to process their private graph data locally while interacting with a centralized server, thus maintaining privacy. However, graph data on clients are typically non-IID, posing a challenge for a single model to perform well across all clients. Another major bottleneck of FGL is the high cost of communication. To address these challenges, we propose a communication-efficient personalized federated graph learning algorithm, CEFGL. Our method decomposes the model parameters into low-rank generic and sparse private models. We employ a dual-channel encoder to learn sparse local knowledge in a personalized manner and low-rank global knowledge in a shared manner. Additionally, we perform multiple local stochastic gradient descent iterations between communication phases and integrate efficient compression techniques into the algorithm. The advantage of CEFGL lies in its ability to capture common and individual knowledge more precisely. By utilizing low-rank and sparse parameters along with compression techniques, CEFGL significantly reduces communication complexity. Extensive experiments demonstrate that our method achieves optimal classification accuracy in a variety of heterogeneous environments across sixteen datasets. Specifically, compared to the state-of-the-art method FedStar, the proposed method (with GIN as the base model) improves accuracy by 5.64\% on cross-datasets setting CHEM, reduces communication bits by a factor of 18.58, and reduces the communication time by a factor of 1.65.

ASWT-SGNN: Adaptive Spectral Wavelet Transform-based Self-Supervised Graph Neural Network

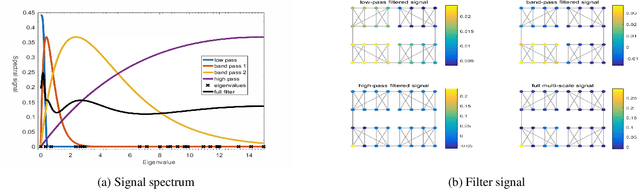
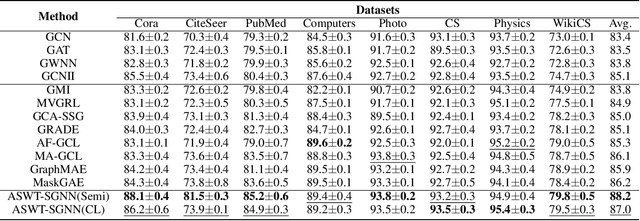
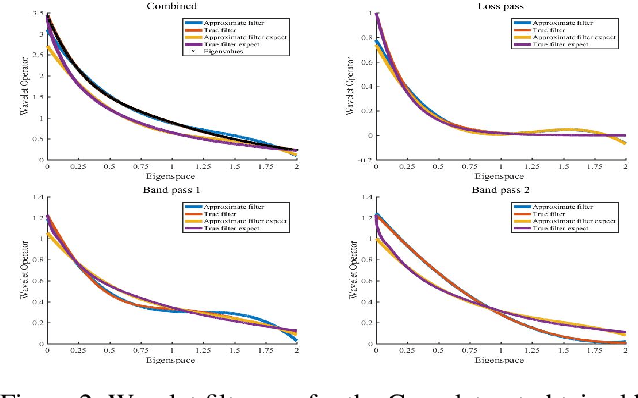
Graph Comparative Learning (GCL) is a self-supervised method that combines the advantages of Graph Convolutional Networks (GCNs) and comparative learning, making it promising for learning node representations. However, the GCN encoders used in these methods rely on the Fourier transform to learn fixed graph representations, which is inherently limited by the uncertainty principle involving spatial and spectral localization trade-offs. To overcome the inflexibility of existing methods and the computationally expensive eigen-decomposition and dense matrix multiplication, this paper proposes an Adaptive Spectral Wavelet Transform-based Self-Supervised Graph Neural Network (ASWT-SGNN). The proposed method employs spectral adaptive polynomials to approximate the filter function and optimize the wavelet using contrast loss. This design enables the creation of local filters in both spectral and spatial domains, allowing flexible aggregation of neighborhood information at various scales and facilitating controlled transformation between local and global information. Compared to existing methods, the proposed approach reduces computational complexity and addresses the limitation of graph convolutional neural networks, which are constrained by graph size and lack flexible control over the neighborhood aspect. Extensive experiments on eight benchmark datasets demonstrate that ASWT-SGNN accurately approximates the filter function in high-density spectral regions, avoiding costly eigen-decomposition. Furthermore, ASWT-SGNN achieves comparable performance to state-of-the-art models in node classification tasks.