Connectome Smoothing via Low-rank Approximations

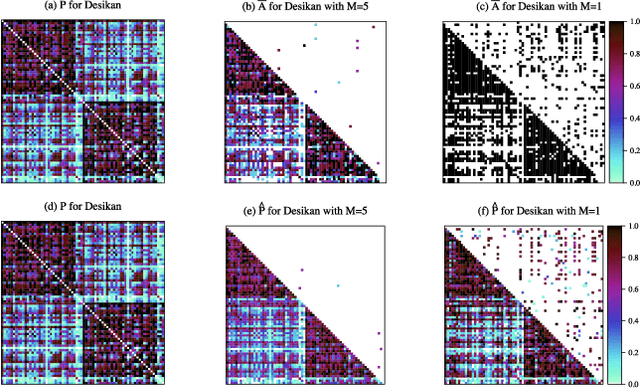
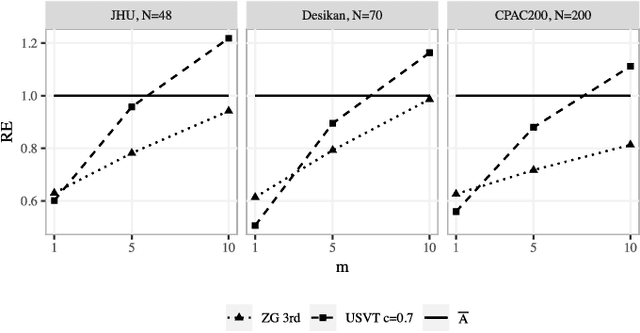
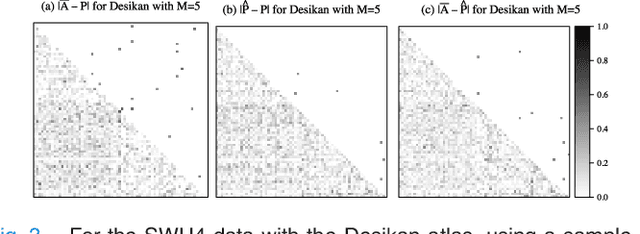
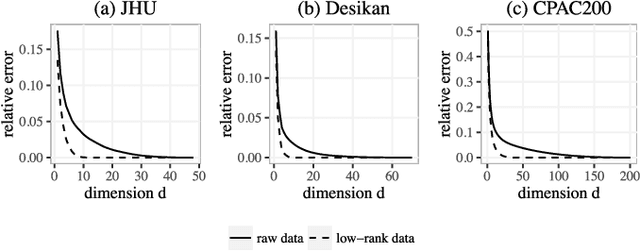
In statistical connectomics, the quantitative study of brain networks, estimating the mean of a population of graphs based on a sample is a core problem. Often, this problem is especially difficult because the sample or cohort size is relatively small, sometimes even a single subject. While using the element-wise sample mean of the adjacency matrices is a common approach, this method does not exploit any underlying structural properties of the graphs. We propose using a low-rank method which incorporates tools for dimension selection and diagonal augmentation to smooth the estimates and improve performance over the naive methodology for small sample sizes. Theoretical results for the stochastic blockmodel show that this method offers major improvements when there are many vertices. Similarly, we demonstrate that the low-rank methods outperform the standard sample mean for a variety of independent edge distributions as well as human connectome data derived from magnetic resonance imaging, especially when sample sizes are small. Moreover, the low-rank methods yield "eigen-connectomes", which correlate with the lobe-structure of the human brain and superstructures of the mouse brain. These results indicate that low-rank methods are an important part of the tool box for researchers studying populations of graphs in general, and statistical connectomics in particular.

Empirical Bayes Estimation for the Stochastic Blockmodel

Inference for the stochastic blockmodel is currently of burgeoning interest in the statistical community, as well as in various application domains as diverse as social networks, citation networks, brain connectivity networks (connectomics), etc. Recent theoretical developments have shown that spectral embedding of graphs yields tractable distributional results; in particular, a random dot product latent position graph formulation of the stochastic blockmodel informs a mixture of normal distributions for the adjacency spectral embedding. We employ this new theory to provide an empirical Bayes methodology for estimation of block memberships of vertices in a random graph drawn from the stochastic blockmodel, and demonstrate its practical utility. The posterior inference is conducted using a Metropolis-within-Gibbs algorithm. The theory and methods are illustrated through Monte Carlo simulation studies, both within the stochastic blockmodel and beyond, and experimental results on a Wikipedia data set are presented.

A model selection approach for clustering a multinomial sequence with non-negative factorization

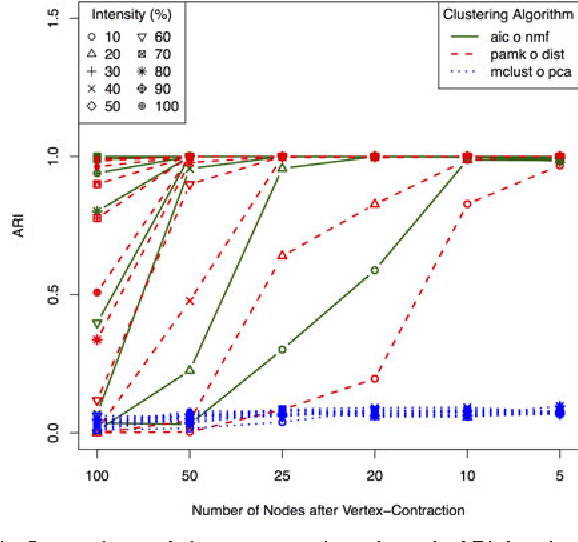
We consider a problem of clustering a sequence of multinomial observations by way of a model selection criterion. We propose a form of a penalty term for the model selection procedure. Our approach subsumes both the conventional AIC and BIC criteria but also extends the conventional criteria in a way that it can be applicable also to a sequence of sparse multinomial observations, where even within a same cluster, the number of multinomial trials may be different for different observations. In addition, as a preliminary estimation step to maximum likelihood estimation, and more generally, to maximum $L_{q}$ estimation, we propose to use reduced rank projection in combination with non-negative factorization. We motivate our approach by showing that our model selection criterion and preliminary estimation step yield consistent estimates under simplifying assumptions. We also illustrate our approach through numerical experiments using real and simulated data.