A model selection approach for clustering a multinomial sequence with non-negative factorization
Paper and Code
Aug 14, 2015
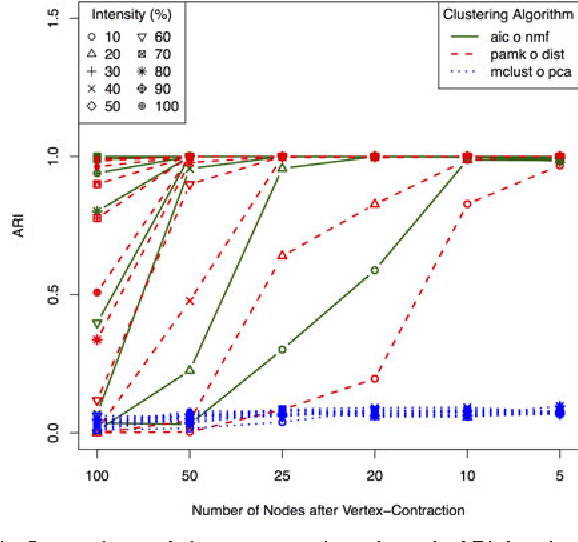

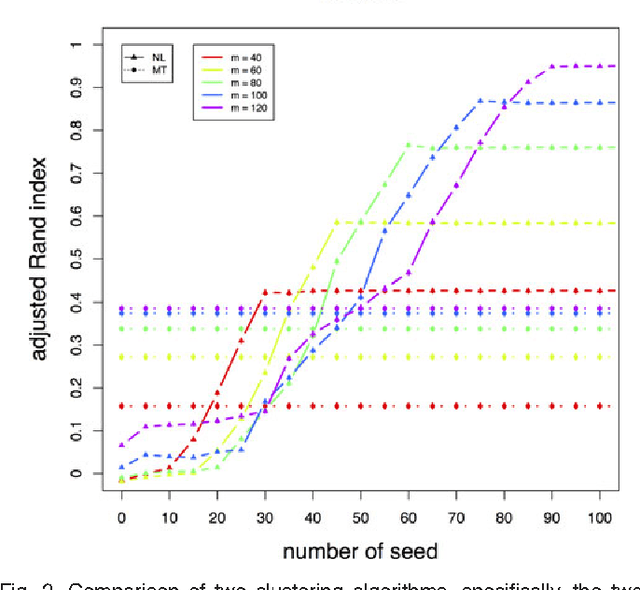
We consider a problem of clustering a sequence of multinomial observations by way of a model selection criterion. We propose a form of a penalty term for the model selection procedure. Our approach subsumes both the conventional AIC and BIC criteria but also extends the conventional criteria in a way that it can be applicable also to a sequence of sparse multinomial observations, where even within a same cluster, the number of multinomial trials may be different for different observations. In addition, as a preliminary estimation step to maximum likelihood estimation, and more generally, to maximum $L_{q}$ estimation, we propose to use reduced rank projection in combination with non-negative factorization. We motivate our approach by showing that our model selection criterion and preliminary estimation step yield consistent estimates under simplifying assumptions. We also illustrate our approach through numerical experiments using real and simulated data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge