ACE: Adaptive Constraint-aware Early Stopping in Hyperparameter Optimization

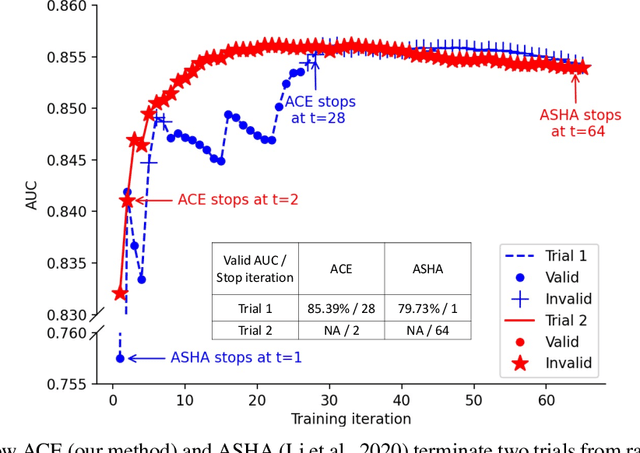
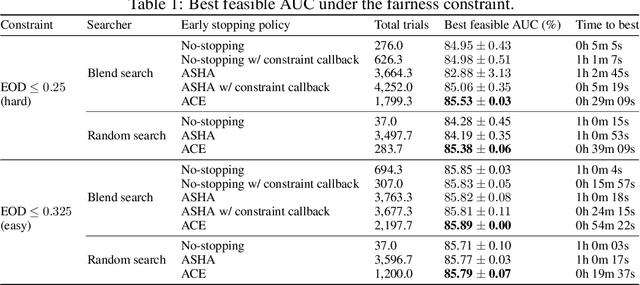
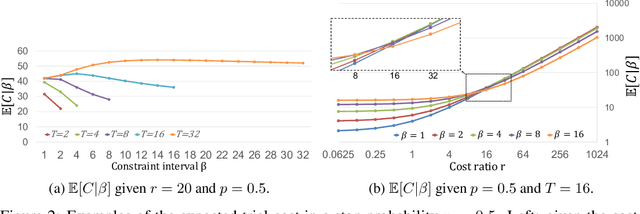
Deploying machine learning models requires high model quality and needs to comply with application constraints. That motivates hyperparameter optimization (HPO) to tune model configurations under deployment constraints. The constraints often require additional computation cost to evaluate, and training ineligible configurations can waste a large amount of tuning cost. In this work, we propose an Adaptive Constraint-aware Early stopping (ACE) method to incorporate constraint evaluation into trial pruning during HPO. To minimize the overall optimization cost, ACE estimates the cost-effective constraint evaluation interval based on a theoretical analysis of the expected evaluation cost. Meanwhile, we propose a stratum early stopping criterion in ACE, which considers both optimization and constraint metrics in pruning and does not require regularization hyperparameters. Our experiments demonstrate superior performance of ACE in hyperparameter tuning of classification tasks under fairness or robustness constraints.

Maximum Regularized Likelihood Estimators: A General Prediction Theory and Applications

Maximum regularized likelihood estimators (MRLEs) are arguably the most established class of estimators in high-dimensional statistics. In this paper, we derive guarantees for MRLEs in Kullback-Leibler divergence, a general measure of prediction accuracy. We assume only that the densities have a convex parametrization and that the regularization is definite and positive homogenous. The results thus apply to a very large variety of models and estimators, such as tensor regression and graphical models with convex and non-convex regularized methods. A main conclusion is that MRLEs are broadly consistent in prediction - regardless of whether restricted eigenvalues or similar conditions hold.