Rui Caseiro
High-Speed Tracking with Kernelized Correlation Filters
Nov 05, 2014
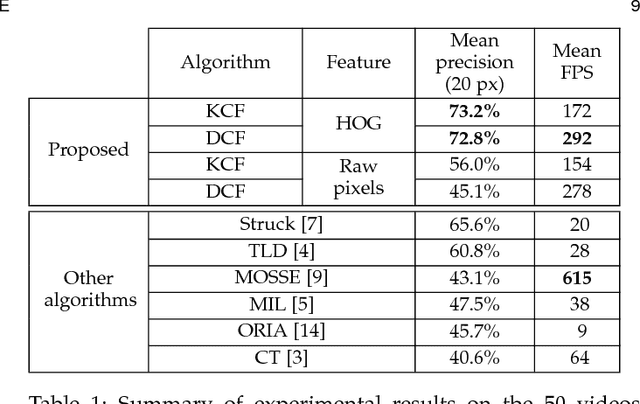

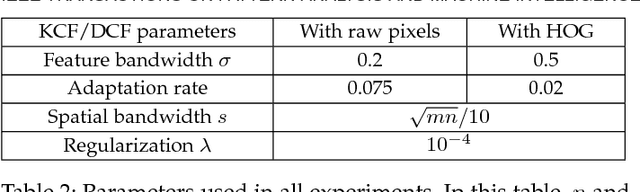
Abstract:The core component of most modern trackers is a discriminative classifier, tasked with distinguishing between the target and the surrounding environment. To cope with natural image changes, this classifier is typically trained with translated and scaled sample patches. Such sets of samples are riddled with redundancies -- any overlapping pixels are constrained to be the same. Based on this simple observation, we propose an analytic model for datasets of thousands of translated patches. By showing that the resulting data matrix is circulant, we can diagonalize it with the Discrete Fourier Transform, reducing both storage and computation by several orders of magnitude. Interestingly, for linear regression our formulation is equivalent to a correlation filter, used by some of the fastest competitive trackers. For kernel regression, however, we derive a new Kernelized Correlation Filter (KCF), that unlike other kernel algorithms has the exact same complexity as its linear counterpart. Building on it, we also propose a fast multi-channel extension of linear correlation filters, via a linear kernel, which we call Dual Correlation Filter (DCF). Both KCF and DCF outperform top-ranking trackers such as Struck or TLD on a 50 videos benchmark, despite running at hundreds of frames-per-second, and being implemented in a few lines of code (Algorithm 1). To encourage further developments, our tracking framework was made open-source.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge