Rosanna Verde
On the use of Wasserstein metric in topological clustering of distributional data
Sep 09, 2021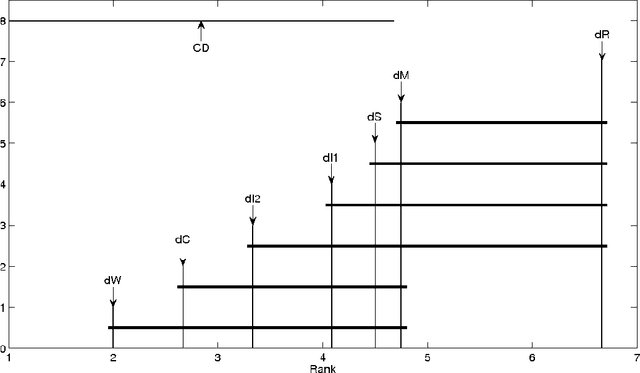
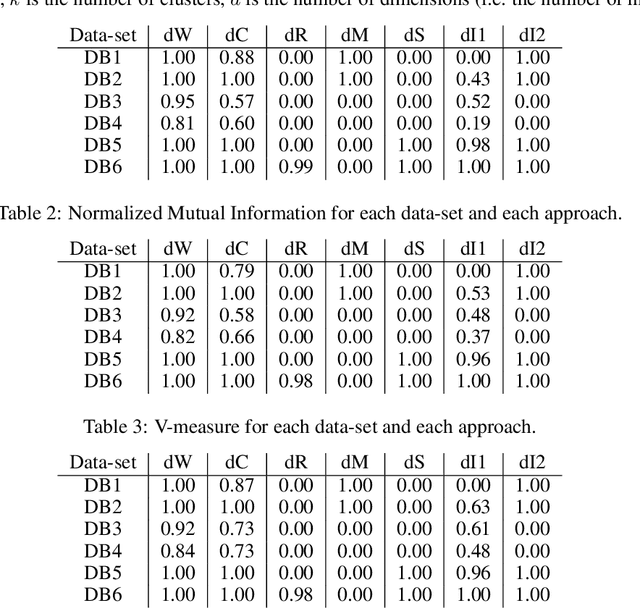
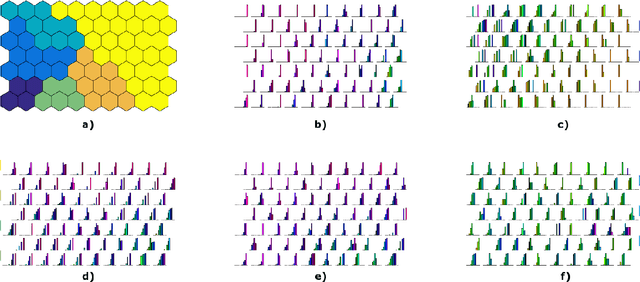
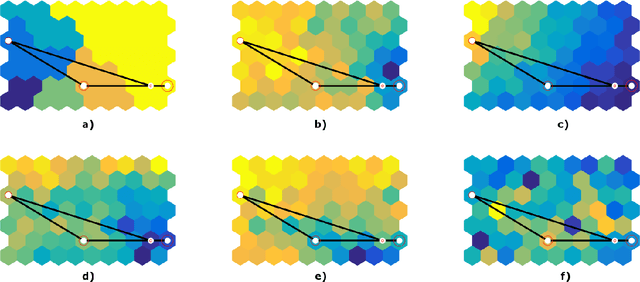
Abstract:This paper deals with a clustering algorithm for histogram data based on a Self-Organizing Map (SOM) learning. It combines a dimension reduction by SOM and the clustering of the data in a reduced space. Related to the kind of data, a suitable dissimilarity measure between distributions is introduced: the $L_2$ Wasserstein distance. Moreover, the number of clusters is not fixed in advance but it is automatically found according to a local data density estimation in the original space. Applications on synthetic and real data sets corroborate the proposed strategy.
Fuzzy clustering of distribution-valued data using adaptive L2 Wasserstein distances
May 02, 2016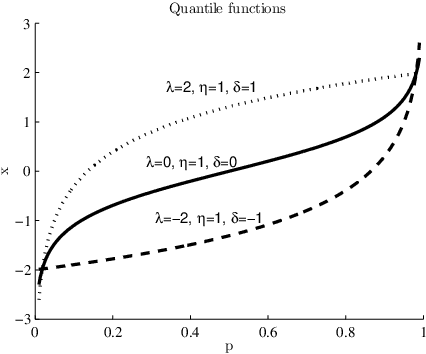

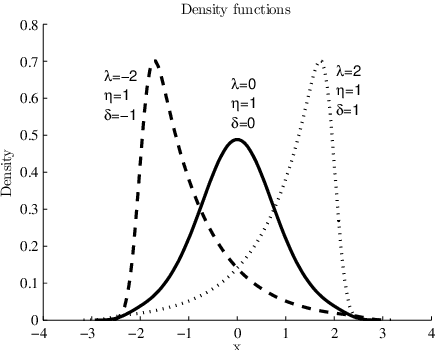
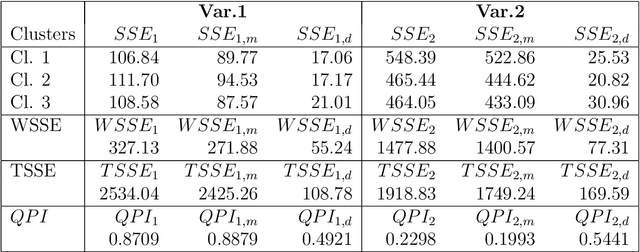
Abstract:Distributional (or distribution-valued) data are a new type of data arising from several sources and are considered as realizations of distributional variables. A new set of fuzzy c-means algorithms for data described by distributional variables is proposed. The algorithms use the $L2$ Wasserstein distance between distributions as dissimilarity measures. Beside the extension of the fuzzy c-means algorithm for distributional data, and considering a decomposition of the squared $L2$ Wasserstein distance, we propose a set of algorithms using different automatic way to compute the weights associated with the variables as well as with their components, globally or cluster-wise. The relevance weights are computed in the clustering process introducing product-to-one constraints. The relevance weights induce adaptive distances expressing the importance of each variable or of each component in the clustering process, acting also as a variable selection method in clustering. We have tested the proposed algorithms on artificial and real-world data. Results confirm that the proposed methods are able to better take into account the cluster structure of the data with respect to the standard fuzzy c-means, with non-adaptive distances.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge