Exploiting Uncertainty for Querying Inconsistent Description Logics Knowledge Bases

The necessity to manage inconsistency in Description Logics Knowledge Bases (KBs) has come to the fore with the increasing importance gained by the Semantic Web, where information comes from different sources that constantly change their content and may contain contradictory descriptions when considered either alone or together. Classical reasoning algorithms do not handle inconsistent KBs, forcing the debugging of the KB in order to remove the inconsistency. In this paper, we exploit an existing probabilistic semantics called DISPONTE to overcome this problem and allow queries also in case of inconsistent KBs. We implemented our approach in the reasoners TRILL and BUNDLE and empirically tested the validity of our proposal. Moreover, we formally compare the presented approach to that of the repair semantics, one of the most established semantics when considering DL reasoning tasks.

Non-ground Abductive Logic Programming with Probabilistic Integrity Constraints

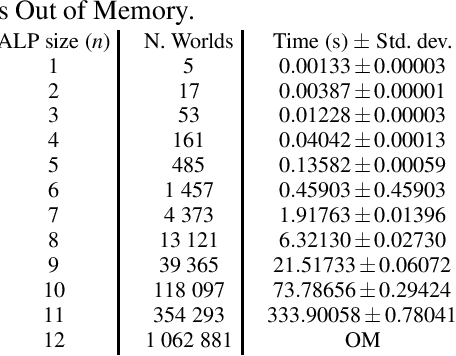
Uncertain information is being taken into account in an increasing number of application fields. In the meantime, abduction has been proved a powerful tool for handling hypothetical reasoning and incomplete knowledge. Probabilistic logical models are a suitable framework to handle uncertain information, and in the last decade many probabilistic logical languages have been proposed, as well as inference and learning systems for them. In the realm of Abductive Logic Programming (ALP), a variety of proof procedures have been defined as well. In this paper, we consider a richer logic language, coping with probabilistic abduction with variables. In particular, we consider an ALP program enriched with integrity constraints `a la IFF, possibly annotated with a probability value. We first present the overall abductive language, and its semantics according to the Distribution Semantics. We then introduce a proof procedure, obtained by extending one previously presented, and prove its soundness and completeness.

A Framework for Reasoning on Probabilistic Description Logics

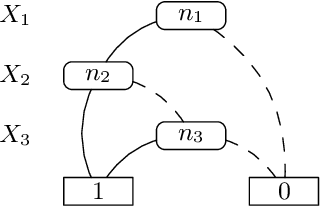
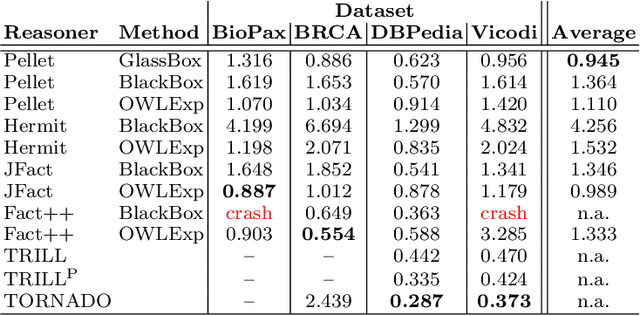
While there exist several reasoners for Description Logics, very few of them can cope with uncertainty. BUNDLE is an inference framework that can exploit several OWL (non-probabilistic) reasoners to perform inference over Probabilistic Description Logics. In this chapter, we report the latest advances implemented in BUNDLE. In particular, BUNDLE can now interface with the reasoners of the TRILL system, thus providing a uniform method to execute probabilistic queries using different settings. BUNDLE can be easily extended and can be used either as a standalone desktop application or as a library in OWL API-based applications that need to reason over Probabilistic Description Logics. The reasoning performance heavily depends on the reasoner and method used to compute the probability. We provide a comparison of the different reasoning settings on several datasets.

MAP Inference for Probabilistic Logic Programming

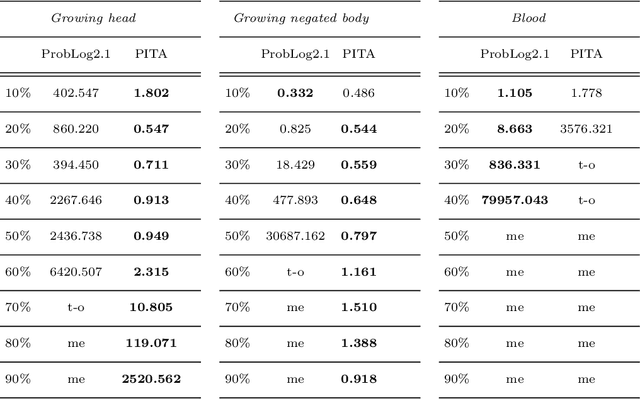
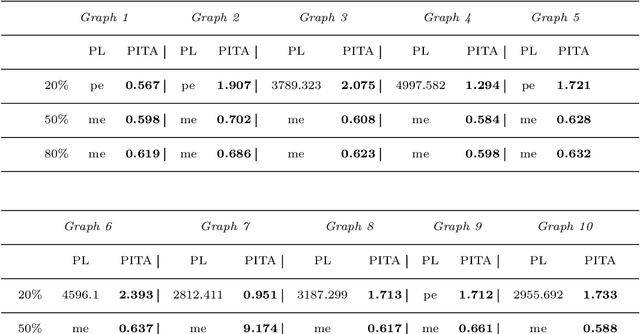
In Probabilistic Logic Programming (PLP) the most commonly studied inference task is to compute the marginal probability of a query given a program. In this paper, we consider two other important tasks in the PLP setting: the Maximum-A-Posteriori (MAP) inference task, which determines the most likely values for a subset of the random variables given evidence on other variables, and the Most Probable Explanation (MPE) task, the instance of MAP where the query variables are the complement of the evidence variables. We present a novel algorithm, included in the PITA reasoner, which tackles these tasks by representing each problem as a Binary Decision Diagram and applying a dynamic programming procedure on it. We compare our algorithm with the version of ProbLog that admits annotated disjunctions and can perform MAP and MPE inference. Experiments on several synthetic datasets show that PITA outperforms ProbLog in many cases.

Probabilistic DL Reasoning with Pinpointing Formulas: A Prolog-based Approach

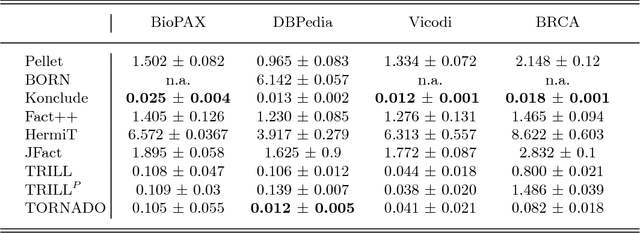
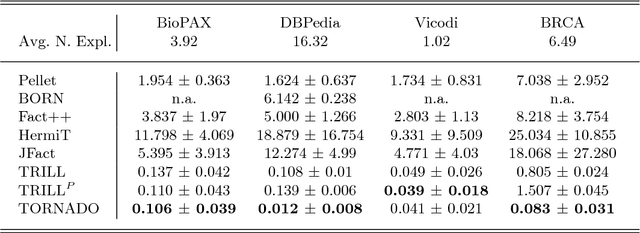
When modeling real world domains we have to deal with information that is incomplete or that comes from sources with different trust levels. This motivates the need for managing uncertainty in the Semantic Web. To this purpose, we introduced a probabilistic semantics, named DISPONTE, in order to combine description logics with probability theory. The probability of a query can be then computed from the set of its explanations by building a Binary Decision Diagram (BDD). The set of explanations can be found using the tableau algorithm, which has to handle non-determinism. Prolog, with its efficient handling of non-determinism, is suitable for implementing the tableau algorithm. TRILL and TRILLP are systems offering a Prolog implementation of the tableau algorithm. TRILLP builds a pinpointing formula, that compactly represents the set of explanations and can be directly translated into a BDD. Both reasoners were shown to outperform state-of-the-art DL reasoners. In this paper, we present an improvement of TRILLP, named TORNADO, in which the BDD is directly built during the construction of the tableau, further speeding up the overall inference process. An experimental comparison shows the effectiveness of TORNADO. All systems can be tried online in the TRILL on SWISH web application at http://trill.ml.unife.it/.

Reasoning with Probabilistic Logics

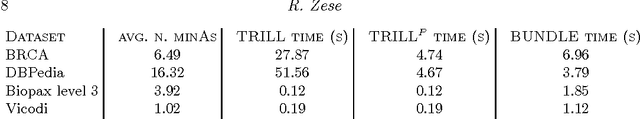
The interest in the combination of probability with logics for modeling the world has rapidly increased in the last few years. One of the most effective approaches is the Distribution Semantics which was adopted by many logic programming languages and in Descripion Logics. In this paper, we illustrate the work we have done in this research field by presenting a probabilistic semantics for description logics and reasoning and learning algorithms. In particular, we present in detail the system TRILL P, which computes the probability of queries w.r.t. probabilistic knowledge bases, which has been implemented in Prolog. Note: An extended abstract / full version of a paper accepted to be presented at the Doctoral Consortium of the 30th International Conference on Logic Programming (ICLP 2014), July 19-22, Vienna, Austria

Lifted Variable Elimination for Probabilistic Logic Programming

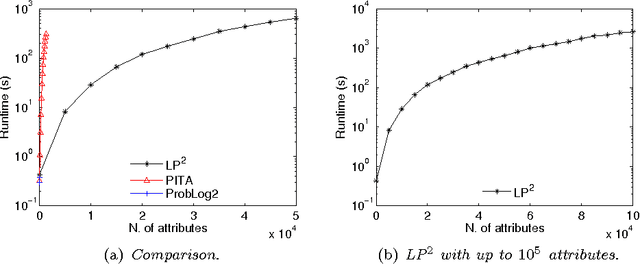
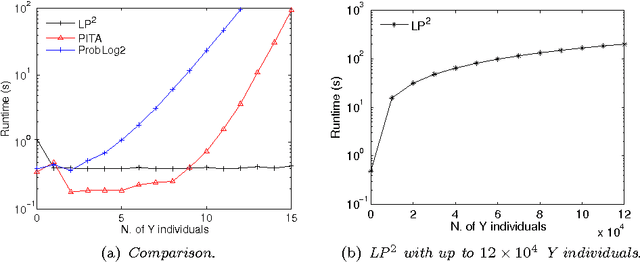
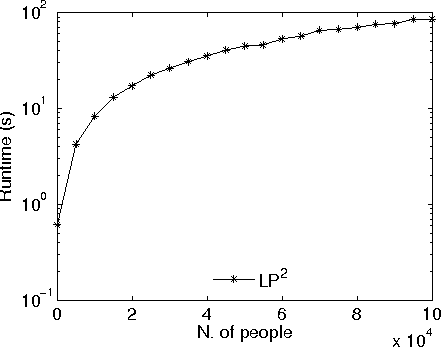
Lifted inference has been proposed for various probabilistic logical frameworks in order to compute the probability of queries in a time that depends on the size of the domains of the random variables rather than the number of instances. Even if various authors have underlined its importance for probabilistic logic programming (PLP), lifted inference has been applied up to now only to relational languages outside of logic programming. In this paper we adapt Generalized Counting First Order Variable Elimination (GC-FOVE) to the problem of computing the probability of queries to probabilistic logic programs under the distribution semantics. In particular, we extend the Prolog Factor Language (PFL) to include two new types of factors that are needed for representing ProbLog programs. These factors take into account the existing causal independence relationships among random variables and are managed by the extension to variable elimination proposed by Zhang and Poole for dealing with convergent variables and heterogeneous factors. Two new operators are added to GC-FOVE for treating heterogeneous factors. The resulting algorithm, called LP$^2$ for Lifted Probabilistic Logic Programming, has been implemented by modifying the PFL implementation of GC-FOVE and tested on three benchmarks for lifted inference. A comparison with PITA and ProbLog2 shows the potential of the approach.